The GWR GmbH develops algorithms and corresponding software for problems in Applied Mathematics and performs contract computations.
Our fields of expertise include:
- Numerical Simulations
- Mathematical Models
- Fast solution of large systems of equations
- C++ programming, in particular
- Parallelization and multicore applications, MPI, OpenMP and Threading Building Blocks
- Flow simulations with OpenFOAM
- Visualizations
- Algorithmic Geometry
-
Cloud Computing:
Scalable HPC environments and automated workflows in the cloud (Azure HPC & Jenkins). - Artificial Intelligence in simulation & software development
-
Physics-Informed Neural Networks (PINNs) & Operator Networks (PINOs):
Modern machine learning models that directly integrate physical laws into neural networks.
PINNs approximate individual solutions of physical equations (functions).
PINOs learn entire solution operators, i.e. mappings between function spaces.
Both approaches combine data-driven methods with physical prior knowledge. -
Further AI-assisted tools are also used in software development, see our example on
AI-assisted commit automation.
-
Physics-Informed Neural Networks (PINNs) & Operator Networks (PINOs):
- Combinatorial optimization.
We use a wide range of programming languages and tools, including C++, Lua, Python, Java and shell scripts. Our software development processes are continuously optimized through the use of Git for version control and Jenkins for automation.
Simulations
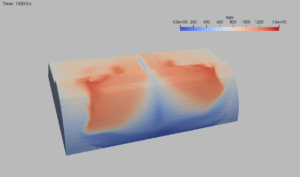
Numerical simulations are used in many application areas – for example in flow simulations in automotive engineering, in finite element analyses for calculating stresses and deformations in components, or in modeling financial markets and weather developments. Many methods are based on mathematical models from physics, which allow complex phenomena to be represented realistically. Increasingly, artificial intelligence methods are also being used, for example to accelerate calculations or to analyze large data sets. Simulations enable virtual experiments that contribute to the development of new products or to the optimization of technical processes – in science, industry, and engineering.
Algorithms
A problem should be solved with the “right” algorithm, as the choice of an appropriate algorithm is crucial for efficiency. An impressive example is the Fast Fourier Transform[1] (FFT). Compared to the direct evaluation of the trigonometric sum formula, it offers a significant improvement. While the naive method requires \(\mathcal{O}(n^2)\) computational steps, the FFT only requires \(\mathcal{O}(n \log n)\).
Our example on modular exponentiation illustrates how the mere choice of method can dramatically speed up runtime. From originally 10 seconds, the computation time is reduced to just a few microseconds.
The importance of choosing a suitable algorithm is also evident in the numerical solution of the radiosity equation for calculating energy transport by thermal radiation as well as in parameter identification – both in terms of stability and computational efficiency.
Programming
Software, especially simulation programs, should be continuously developed in order to exploit the full potential of the available hardware. Special software techniques such as OpenMP and Threading Building Blocks for multicore architectures as well as SYCL for cross-platform programming (CPU + GPU) play a decisive role here. These techniques enable efficient use of modern hardware and help maximize the performance of applications.