\(
\def\x{{\bf x}}
\def\y{{\bf y}}
\newcommand{\Spro}[2]{\langle {#1},{#2} \rangle}
\)
Mehrgitterverfahren sind in der Lage große Gleichungssysteme mit mehreren Millionen Unbekannten, die sich aus der Diskretisierung von physikalischen Simulationsmodellen ergeben und bestimmte Anforderungen erfüllen, schnell zu lösen. Im Gegensatz zu klassischen Iterationsverfahren, deren Konvergenzrate mit zunehmender Feinheit des Gitters abnimmt, behalten Mehrgittermethoden ihre guten Konvergenzeigenschaften auch für sehr feine Gitter bei.
Die Diskretisierung der Randwertaufgabe
\begin{equation} \label{eq1}
– \Delta u ({\bf x}) = f ({\bf x}) , \qquad {\bf x}\in \Omega , \qquad u\Big|_{\partial \Omega} = g
\end{equation}
auf einem Gitter $\Omega_{H} :=\{ \x^i \; :\; \x^i \text{ist Knoten der geometrischen Modellierung} \}$ ergebe, z.B. mittels FEM-Verfahren, ein Gleichungssystem
\begin{equation}
A_H \, x_H = f_H \label{eq2}
\end{equation}
mit positiv definiter Matrix $A_H$. Durch Halbierung der Schrittweite $H$, d.h. Verfeinerung des Gitters $\Omega_H$, erhält man ein weiteres Gleichungssystem, das die gleiche Struktur wie $\eqref{eq1}$, jedoch die 4-fache Dimension, aufweist. Die Approximation der Lösung von $\eqref{eq1}$ durch den Ansatz verbessert sich, jedoch wächst der Aufwand zur Lösung des entsprechenden Gleichungssystems.
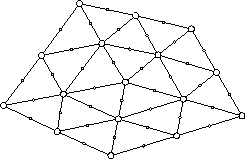
Verfeinerung mit $h=H/2$
Sei nun $x_h^{\star}$ die Lösung des Gleichungssystems $A_h \, x_h = f_h$ im Gitter $\Omega_h$ und $\tilde{x}_h$ eine Näherung der
Lösung. Es gilt somit
$$ A_h (\tilde{x}_h – x_h^{\star}) = A_h \, \tilde{x}_h – f_h := d_h.$$
Der Vektor $d_h$ ist der Defekt und
$$
e_h := \tilde{x}_h – x_h^{\star}
$$
der Fehler zwischen Näherung und Lösung. Insbesondere folgt die Defektgleichung
\begin{equation}
A_h \, e_h = d_h, \qquad \mbox{ bzw. } \qquad e_h = A_h^{-1} d_h . \label{eq3}
\end{equation}
Ist durch Lösung des Ersatzgleichungssystems der Fehler $e_h$ bekannt, so ergibt sich die gesuchte Lösung sofort durch
\begin{equation}
x_h^{\star} = \tilde{x}_h – e_h. \label{eq4}
\end{equation}
Restriktion und Prolongation
Im Vergleich zur Ausgangssituation ist nichts gewonnen, da die Lösung von $\eqref{eq3}$ genauso schwierig (aufwendig) ist, wie die der Gleichung $A_h \, x_h = f_h$. Der entscheidende Gedanke ist nun, die Defektgleichung auf das grobe Gitter $\Omega_H$ mittels einer Abbildung $r: \Omega_h \longrightarrow \Omega_H$ (Restriktion) zu übertragen:
\begin{equation}
A_H \, e_H = (r \, d_h) \label{eq5}
\end{equation}
und nach $e_H$ aufzulösen: $e_H = A_H^{-1}r \, d_h$. Der Defekt $d_h$ wird also (in geeigneter Weise) auf das grobe Gitter “transportiert”. Die anschließende Lösung des Gleichungsystems $\eqref{eq5}$ ist weniger aufwendig, als die der ursprünglichen Gleichung. Für ein 2D-Problem hat man $\dim A_H = (\dim A_h)/4.$
Eine neue Näherung ergibt sich nun durch
\begin{equation}
x_h^{\rm new} := \tilde{x}_h – p \, e_H, \label{eq6}
\end{equation}
wobei die Abbildung $p$ (die Prolongation) die Korrektur $e_H$ auf das feine Gitter überträgt. Sind $r_h$ und $p_h$ die Matrixdarstellungen der Restriktion und Prolongation, so wird häufig
\begin{equation}
r_h = \sigma \, p_h^T \label{eq7}
\end{equation}
gewählt, dabei is $\sigma$ ein Skalierungsfaktor. Implizit geht hier die Wahl der Diskretisierung (Finite-Elemente-Methode, Finite-Differenzen-Verfahren) und der Skalarprodukte für die Vektoren auf den verschiedenen Gittern ein.
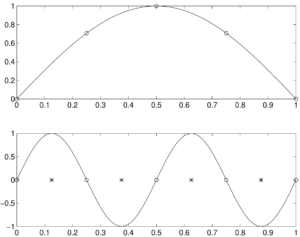 |
Ausgehend vom groben Gitter $\Omega_H$ läßt sich die Menge der Vektoren $X_h$ (auch Menge der Gitterfunktionen genannt) zum feinen Gitter $\Omega_h$ in zwei Kategorien einordnen
- die Menge der hochfrequenten Gitterfunktionen $X_{h.\rm oz}$: diese haben eine “schlechte” Darstellung auf dem groben Gitter und
- die Menge der niederfrequenten Gitterfunktionen $X_{h,glatt}= X_h \setminus X_{h,\rm oz}$: “gute” Darstellung auf dem groben Gitter
Ein Vektor $x_h \in X_h$ kann also in hoch- und niederfrequente Anteile zerlegt werden
\begin{equation}
x_h = \sum_{e_i \in X_{h,\rm glatt}} \alpha_i \, e_i + \sum_{e_j \in X_{h.\rm oz}} \alpha_j \, e_j .
\end{equation}
Glättung
Da es (hochfrequente) Feingitterfunktionen gibt, die das grobe Gitter nicht “sieht”, bildet das durch $\eqref{eq6}$ gegebene Verfahren i.a. keine konvergente Iteration. Die folgende Beobachtung hilft an dieser Stelle entscheidend weiter: Klassische Iterationsverfahren, wie etwa das Gauß-Seidel-Verfahren, haben gerade Probleme die niederfrequenten Anteile in der Lösung zu erfassen, reduzieren aber die hochfrequenten Fehleranteile gut.
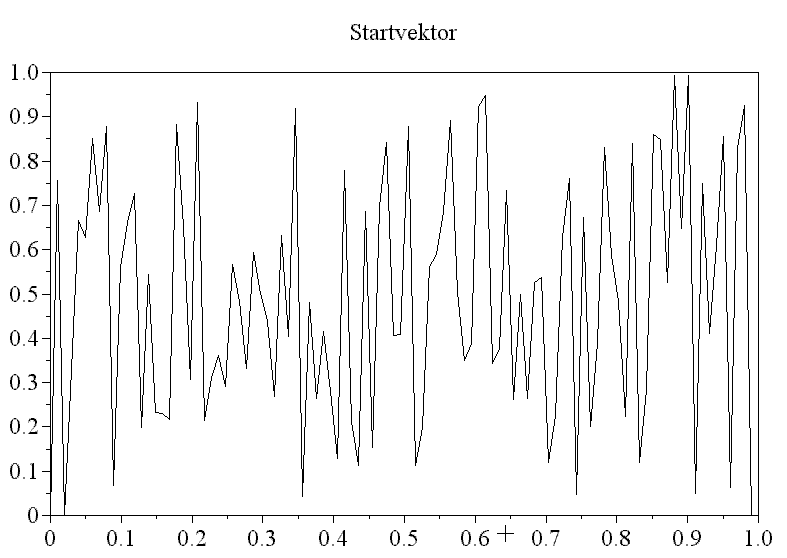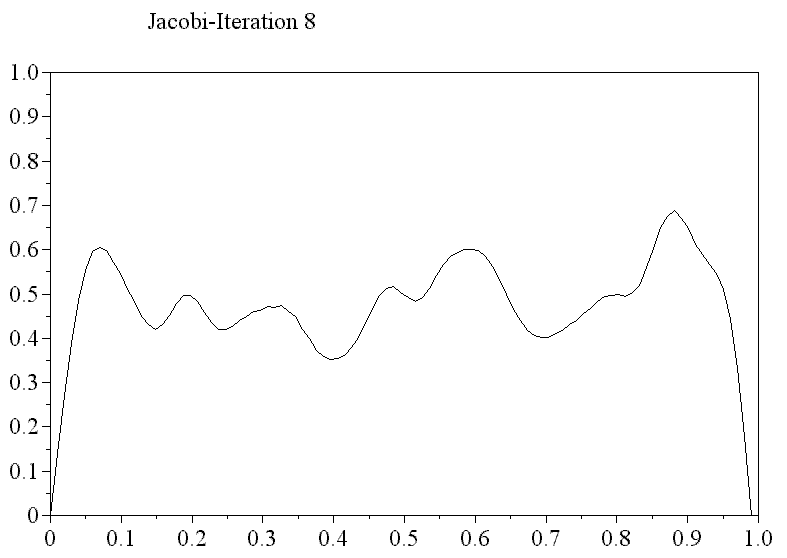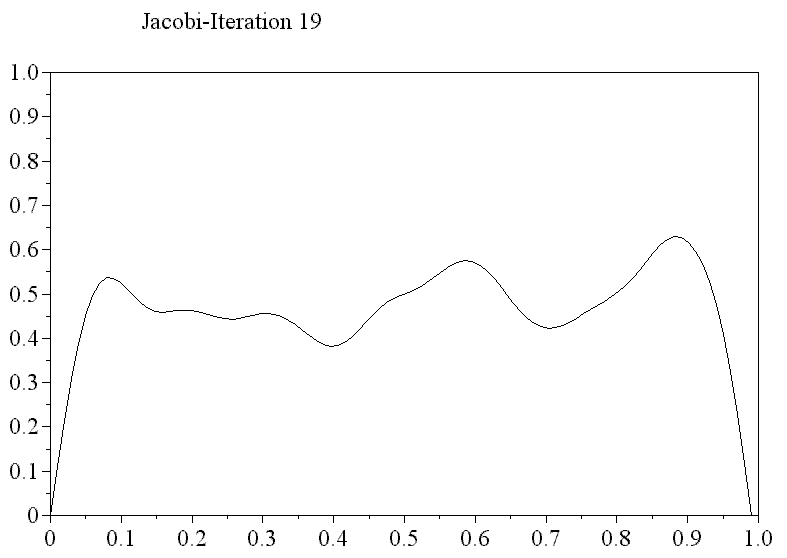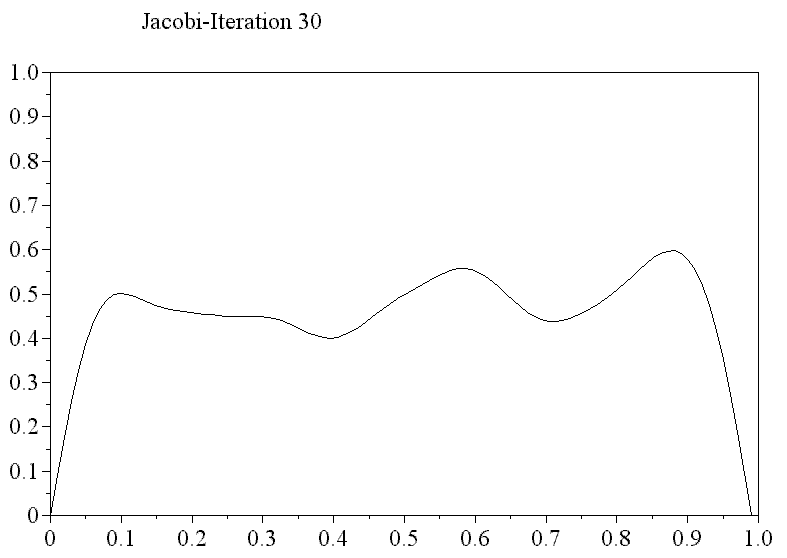
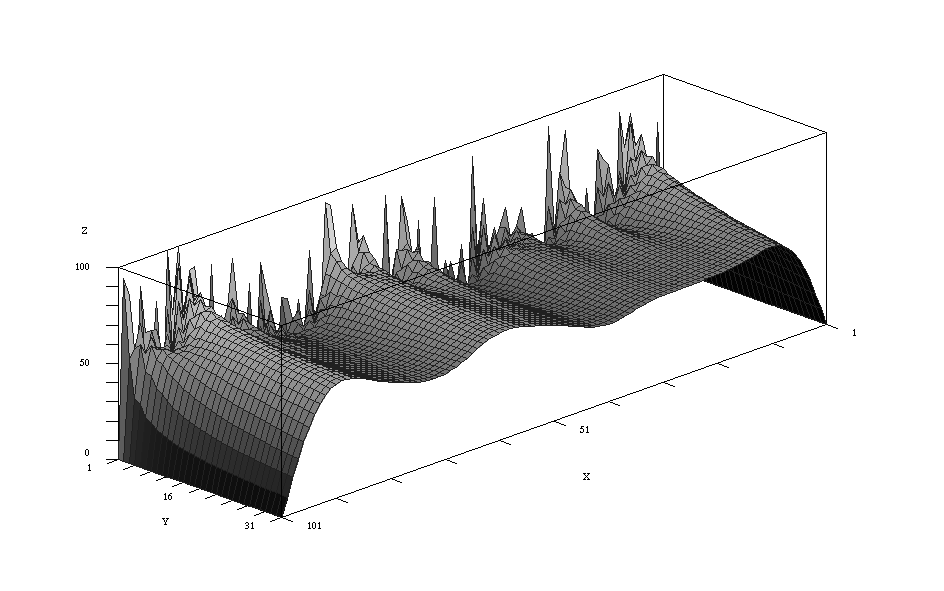
Darstellung des Fehler zu einem 1D-Modellproblem bgzl. des Jacobi-Verfahrens : der hochfrequenten Anteil wird schnell gedämpft, die niederfrequenten Anteile in der Lösung hingegen nur langsam (unten: $e_h(x,y)$, wobei $y$ die Nummer der Jacobi-Iteration ist).
Zweigitterverfahren
Eine Kombination aus klassischem Iterationsverfahren und der Grobgitterkorrektur $\eqref{eq6}$ ergibt das Zweigitterverfahren:
- Glättung: führe einige Schritte (meist weniger als vier) mit einem geeigneten Iterationsverfahren durch
- Grobgitterkorrektur: berechne eine neue Näherung mittels $\eqref{eq5}$
- falls $\| A_h x_h^{new} – f_h \| < tol$ oder eine maximale Anzahl von Iterationen überschritten ist: Stop; sonst gehe zu 1.
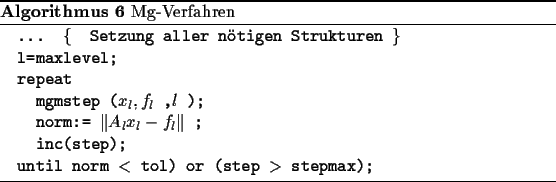
Algorithmus 3 beschreibt ein Unterprogramm, das einen Zweigitterschritt ausführt, und Algorithmus $4$ die Zweigitteriteration.
\begin{eqnarray*}
& \qquad & {\bf \text{ Algorithmus 3 }} \text{zgmstep}(\text{Gp& } x_h, \text{const Gp } f_h, \text{const int } l) & \\
& \qquad & \qquad x_h := S_l (x_h,f_h) & \text{//} \quad l \; \text{ Glättungsschritte (z.B. Jacobi oder Gauss-Seidel) } \\
& \qquad & \qquad d_h := A_h \, x_h -f_h; & \text{//} \quad \text{ Defekt } \\
& \qquad & \qquad d_H := r\, d_h; & \text{//} \quad \text{ Restriktion } \\
& \qquad & \qquad e_H := A_H^{-1} \, d_H; & \text{//} \quad \text{ Grobgitterlösung }\\
& \qquad & \qquad x_h := x_h -p_h \, e_H; & \text{//} \quad \text{ Grobgitterkorrektur }\\
& & & \\
& \qquad & {\bf \text{ Algorithmus 4 }} \text{Mehrgitterverfahren } & \\
& \qquad & \qquad \text{ … } & \ \text{//} \quad \text{ Setzung aller notwendigen Strukturen } \\
& \qquad & \quad {\bf\text{repeat} } & \\
& \qquad & \quad \qquad \text{zgmstep}(x_h, f_h,l); & \\
& \qquad & \quad \qquad \text{norm} :=|| A_l \, x_l – f_l\||; & \\
& \qquad & \quad \qquad ++\text{step}; & \\
& \qquad & \quad {\bf\text{until } } (\text{norm} < \text{tol}) \; \text{or} \; (\text{step} > \text{maxsteps}); &
\end{eqnarray*}
Dabei ist
\begin{equation}
{\cal S}_l (x_h,f_h) := S_h \ x_h + N_h \, f_h
\end{equation}
eine konsistente Iteration, die zur Glättung benutzt wird. Ist diese die Jacobi-Iteration, so gilt
\begin{equation}
S_h =I_h – D_h^{-1} A_h , \qquad N_h=D_h^{-1}, \quad D_h:=diag(A_h).
\end{equation}
Iterationsmatrix
Ausgehend von einer Näherung $x_i$ kann ein Schritt (also die Berechnung der nächsten Iterierten) im eben beschriebenen Zweigitterverfahren auch als lineares Iterationsverfahren
\begin{equation}
x^{(i+1)} = S_h x^{(i)} – p_h A_H^{-1} r_h \left(A_h S_h x_h^{(i)} – \tilde{f}_h \right)
\end{equation}
geschrieben werden. Die Iterationsmatrix des Zweigitterverfahrens ist also
\begin{equation}
M_h^{\rm ZGM} := \left( I_h – p_h \ A_H^{-1} \, r_h \, A_h \right) \, S_h.
\end{equation}
Mit Hilfe von Annahmen über die Regularität der Lösung der zu Grunde liegenden partiellen Differentialgleichung, weiterer Voraussetzungen an die Diskretisierung (geschachtelte Unterräume, Approximationseigenschaften) und an die Glättungsiteration $\mathcal{S}_l$ kann gezeigt werden, daß der Spektralradius der Iterationsmatrix $M_h^{\rm ZGM}$ unabhängig von der Schrittweite h ist:
\begin{equation}
\rho( M_h^{\rm ZGM}) \leq \zeta(\alpha) < 1 , \qquad \mbox{f.a.} \quad \alpha \geq \alpha_0.
\end{equation}
Mehrgitterverfahren
Das Verfahren 4 konvergiert demnach, unter hier nicht näher genannten Voraussetzungen, unabhängig von $h$. Der Übergang vom Zweigitter- zum Mehrgitterverfahren ist jetzt nur noch ein kleiner Schritt: das exakte Lösen der Grobgittergleichung wird nun wiederum durch ein Zweigitterverfahren ersetzt, usw. Die sehr guten Konvergenzeigenschaften bleiben dabei erhalten und es zeigt sich, daß der Aufwand optimal. Das Unterprogramm, das einen Mehrgitterschritt ausführt kann folgendermaßen beschrieben werden
Die Mehrgitteriteration ist dann
Die angesprochenen Themenbereiche können in Hackbusch[1] nachgelesen werden. Eine tiefergehende Darstellung der Mehrgitterverfahren findet sich in Hackbusch[2].
Beispiel: 2D-Modellproblem mit $\Omega=[0,1]$, $g=0$ und $f(x,y)= sin(x \, \pi)* sin(y*\pi)$
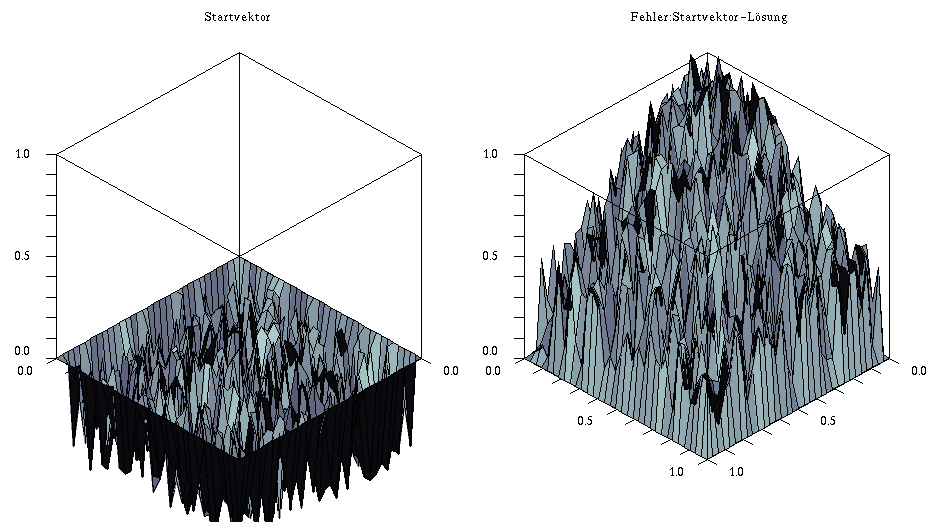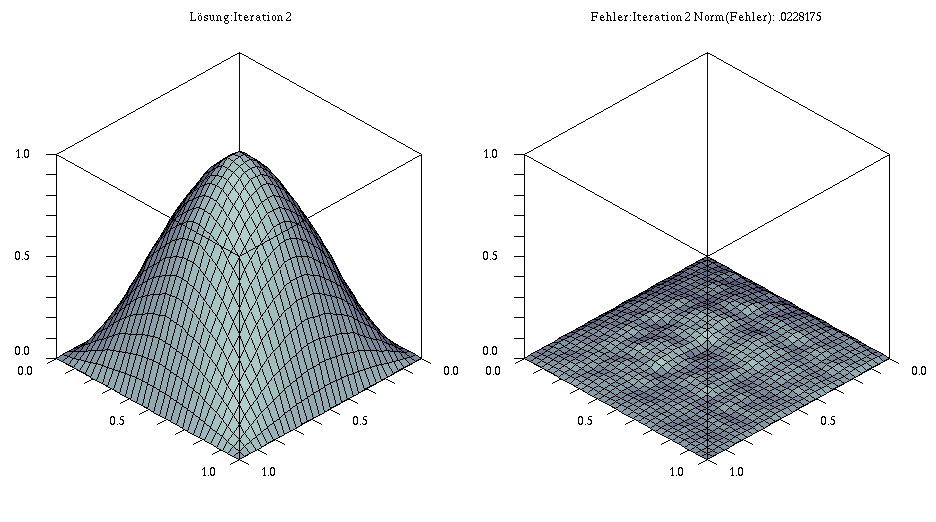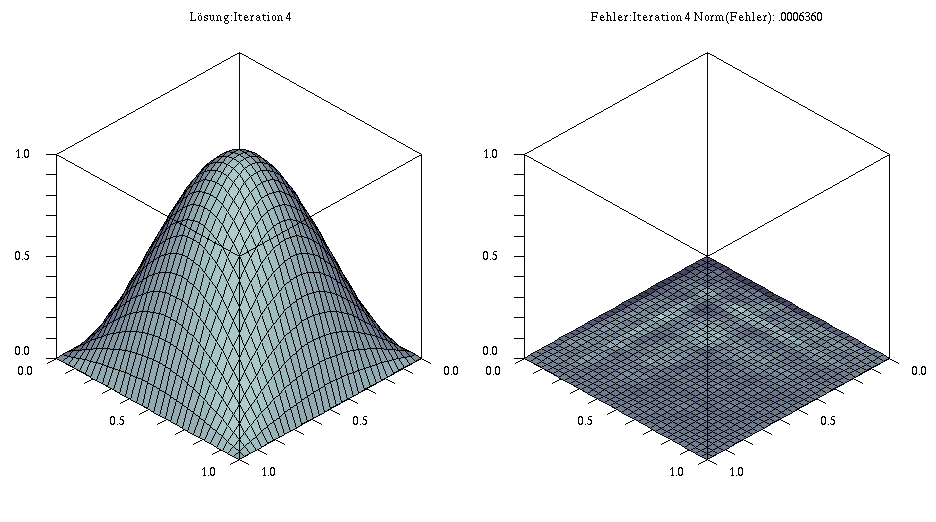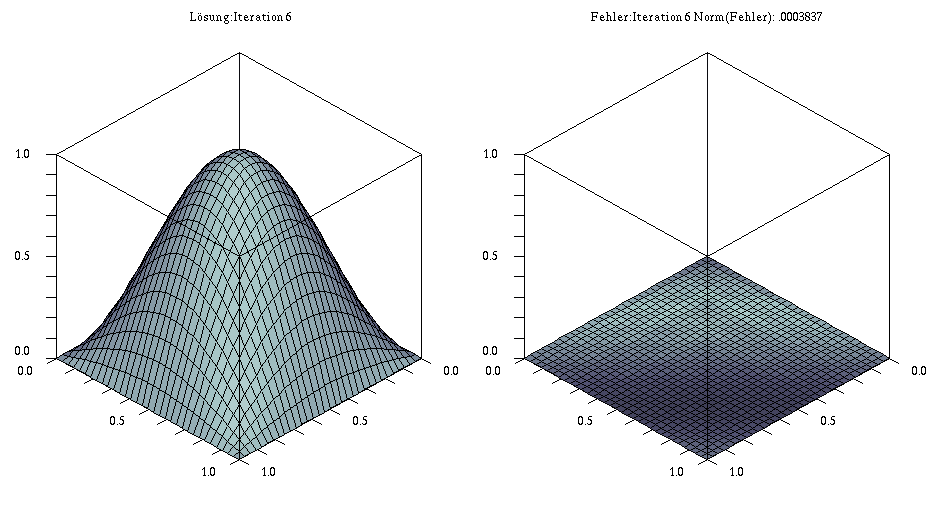
- Diskretisierung: 33×33 Gitter
- Startvektor: x=random
- maxlevel=5, $\gamma=1$
- Glättung: zwei Gauß-Seidel-Iterationen
- Konvergenzrate: 0.2
Quellen
- (1991): Iterative Lösung großer schwachbesetzter Gleichungssysteme. Teubner, Stuttgart, 1991.
- (1985): Multi-grid methods and applications. Springer, Berlin, 1985, ISBN: 978-3-540-12761-1.