\(
\newcommand{\Mod}[1]{\ \mathrm{mod}\ #1}
\)
Für einen Primzahltest, basierend auf den kleinen Fermatscher Satz, wird die Auswertung von $$ a^{p-1} \Mod{p}, \qquad 0 < a < p , \quad a,p \in \mathbb{N} $$ für große Zahlen $a$ und $p$ benötigt. Diese Operation nennt man diskrete Exponentialfunktion oder modulare Exponentiation. Die naive Berechnung, bei der zunächst $a^{p-1}$ vollständig bestimmt und anschließend die Modulo-Operation ausgeführt wird, ist jedoch aussichtslos: sind $a$ und $p$ 10-stellig, dann besitzt $a^p$ schon 100 Milliarden Stellen. Allein die Speicherung einer solchen Zahl würde je nach Darstellung zwischen 40 und 100 GB Speicherplatz benötigen.
Rechenregeln
Die Rechenregeln für Kongruenzen erweisen sich als nützlich beim Modularen Potenzieren. Durch ihre Anwendung wird die effiziente Berechnung, selbst bei großen Zahlen a und p, ermöglicht. Für die Addition modulo $N$ gilt
\begin{equation}
(a + b) \Mod{N} = ( (a \Mod{N}) + (b \Mod{N}) ) \Mod{N}\end{equation} und genauso hat man für die Multiplikation
\begin{equation} \label{modmult}
(a * b) \Mod{N} = ( (a \Mod{N}) * (b \Mod{N}) ) \Mod{N} .
\end{equation} Es gilt also $$a^{n} \Mod{N} = (a \, a^{n-1}) \Mod{N} = ( (a \Mod{N}) \, (a^{n-1} \Mod{N}) ) \Mod{N}. $$
Iteratives Verfahren
Die wiederholte Anwendung von \eqref{modmult} zur Bestimmung von $a^n \Mod{m}$ ergibt das iterative Verfahren:
typedef long long LongInt;
// berechnet a^n mod m
LongInt modular_expo(const LongInt& base, const LongInt& exponent,const LongInt& modulus){
LongInt result = 1;
for (LongInt k=0; k < exponent; ++k)
result = ( result * base) % modulus;
return result;
}
Der Aufwand[1] ist $\mathcal{O}(n)$. Diese Komplexität wäre i. Allg. für viele (andere) Verfahren schon sehr gut. Für das vorliegende Problem geht es aber noch besser.
Ein $\mathcal{O}(\log_2 N)$-Verfahren
Nutzen wir den Zusammenhang \[ a^n = a^{\frac{n}{2}} \cdot a^{\frac{n}{2}} \quad \text{für gerades } n, \] dann ergibt sich direkt:
Divide & Conquer:
\[
\begin{aligned} a^n \mod N &= \left(a^{\frac{n}{2}} \cdot a^{\frac{n}{2}} \right) \mod N \\
&= \left( a^{\frac{n}{2}} \mod N \right) \cdot \left( a^{\frac{n}{2}} \mod N \right) \mod N \\
&= \left( \left(a^{\frac{n}{2}} \mod N \right)^2 \right) \mod N
\end{aligned} \]
Die Aufgabe wurde in zwei identische Teilprobleme halber Länge zerlegt – typisches Prinzip von Divide & Conquer. Der Aufwand beträgt nur noch $\mathcal{O}(n/2)$:
if ( exponent % 2 ==0) {
LongInt zw = modular_expo(base, exponent/2,modulus);
result = (zw*zw) % modulus;
}
Das Vorgehen kann rekursiv fortgesetzt werden.
LongInt modular_expo_faster(const LongInt &base, const LongInt &exponent,const LongInt &modulus){
if ( exponent == 2) return (base*base) % modulus;
if ( exponent == 0) return 1;
if ( modulus == 1) return 0;
LongInt result = 1;
if ( exponent % 2 ==0) { // exponent gerade
LongInt zw = modular_expo_faster(base, exponent/2,modulus) % modulus;
result = (zw*zw) % modulus;
}
else { // exponent ungerade
result = (base % modulus);
result = (result * ( modular_expo_faster(base, exponent-1,modulus) % modulus) ) % modulus;
}
return result;
}
Der Aufwand für diesen Algorithmus ist von der Größenordnung $\mathcal{O}(\log_2 N)$. Das ist gegenüber der ersten Version eine wesentliche Verbesserung.
Vergleiche
Die nachfolgenden Tabellen zeigen, welchen enormen Vorteil bzgl. der Rechenzeit die “divide and conquer”-Variante hat. Für die Beispiele aus den Tabellen wurden zufällig Zahlen aus dem Bereich $(2,10^6)$ für die Basis $a$ und aus unterschiedlichen Intervallen ungerade Zahlen für den Exponenten $N$ gewählt. Ein möglicher integer overflow wird in beiden Algorithmen nicht berücksichtigt.
$0< N < 10^{8}$: der zweite Algorithmus ist 100000-fach(!) schneller
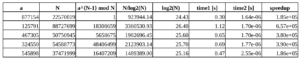
Mit 22570019 wird hier eine Primzahl[2] “gefunden”. Sind für $N$ Zahlen bis $10^{9}$ zugelassen, dann ist das rekursive Verfahren sogar um den Faktor $10^6$ schneller.

Für $N<10^{10}$ benötigt eine Auswertung des iterativen Verfahrens schon mehr als eine Minute Rechenzeit.

Alle Testrechnungen wurden auf einem PC mit i7-5820K, 3.30GHz, CPU durchgeführt (g++ 8.2, C++, 1 Thread).
SageMath-Script
Links zu dem Thema: