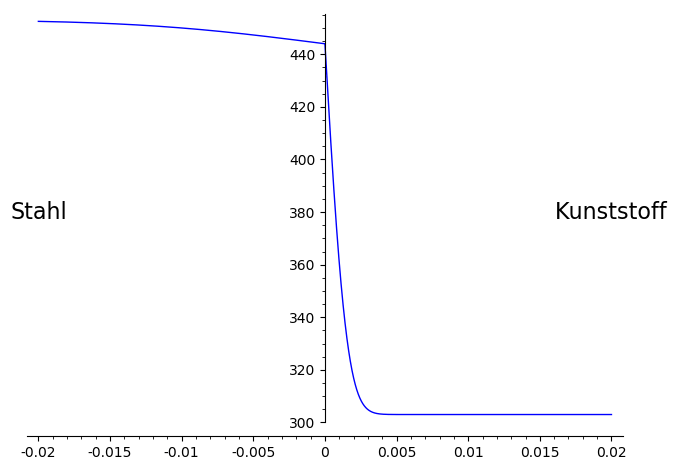
1D-Interface Problem
Der Temperaturverlauf in der Umgebung eines Kontaktbereiches wird mithilfe des nachfolgenden Modellproblems analysiert (1D-Interface Problem). Für die numerische Lösung der heat equation in komplizierten 3-D-Geometrien lassen sich hiermit Rückschlüsse zur Auflösung des evtl. großen Temperaturgradienten (Feinheit des Gitters im Kontaktbereich) bzw. zur Konstruktion von Ansatzfunktionen fürs XFEM-Verfahren gewinnen. Das Modellproblem […]