In diesem Beitrag beschreibe ich die Entwicklung und Implementierung eines einfachen neuronalen Netzwerks, das die Sinusfunktion approximieren kann. Die Methodik folgt hierbei den physikalisch informierten neuronalen Netzen (PINNs), welche maschinelles Lernen mit physikalischen Gesetzen kombinieren, um Modelle zu erstellen, die physikalische Prinzipien einhalten. PINNs haben den großen Vorteil, dass sie keine externen Trainingsdaten benötigen, da die physikalischen Gesetze (PDEs, Erhaltungsgesetze) direkt in die Verlustfunktion implementiert sind. Die erforderlichen Daten werden somit durch die physikalischen Gesetze selbst erzeugt.
Im Beispiel betrachten wir zunächst die Sinusfunktion im Intervall von 0 bis \(2 \, \pi\). Die Zielwerte sind die entsprechenden Sinuswerte dieser Datenpunkte, die dann in die Verlustfunktion, den Standard-Fehler (Mean Squared Error), aufgenommen werden. Das Netzwerk besteht aus mehreren voll verbundenen Schichten, das Training erfolgt mithilfe des Adam-Optimierers. Später verwende ich auch eine benutzerdefinierte Verlustfunktion, die sowohl den Standard-Fehler als auch einen Periodizitätsfehler berücksichtigt. Letzterer sorgt dafür, dass das Netzwerk die periodische Natur der Sinusfunktion lernt.
Warum die Sinusfunktion als Beispiel
Die Wahl der Sinusfunktion als Beispiel hat mehrere Gründe:
- Einfachheit der Zielfunktion: Zunächst sollte überhaupt ein Physics-Informed Neural Network (PINN) mit C++ und libtorch [1] laufen. Daher fiel die Wahl auf eine sehr einfache Zielfunktion, um die Implementierung zu erleichtern. Kompliziertere Verlustfunktionen mit PDEs (z.B. Heat-equation) folgen später.
- Diskussion über das Verhalten außerhalb des Trainingsintervalls: Diese Funktion ist auch deshalb interessant, da Stephen Wolfram[2] ihr Verhalten außerhalb des Trainingsintervalls diskutiert.
- Testrechnungen bezüglich des Frequenz-Prinzips: Die Sinusfunktion ermöglicht auch einfache Testrechnungen in Bezug auf das Frequenz-Prinzip, was zusätzliche Erkenntnisse über die Einsatzmöglichkeiten der PINNs liefert. Ein Anwendungsfall könnte die Verwendung ähnlich der Grobgitterkorrektur im Mehrgitterverfahren sein.
Hauptprogramm train
Der Quelltext ist in kleinere Blöcke unterteilt, um die einzelnen Aktionen zu beschreiben.
Initialisierung und Setup
Der erste Block des Programms initialisiert die notwendigen Bibliotheken und definiert die Hauptfunktion. Außerdem legen wir hier die Optimierungsschritte und die Toleranz fest.
#include <iostream>
#include <torch/torch.h>
#include <fstream>
#include "net.h"
// Beschreibung der Argumente:
// ---------------------------
// 1. optiSteps (optional): Anzahl der Optimierungsschritte (Standard: 20000).
// 2. tol (optional): Toleranz fuer den Verlustwert, bei dem die Optimierung
// gestoppt wird (Standardwert: 1.0e-6).
//
using namespace std;
int main(int argc, char *argv[])
{
int optiSteps = 20000;
double tol = 1.0e-6;
if (argc > 1)
optiSteps = atoi(argv[1]);
if (argc == 3)
tol = atof(argv[2]);
Modell und Optimierer
In diesem Block wird das Modell und der Optimierer initialisiert. Wir erstellen das Modell als shared pointer und konfigurieren den Adam-Optimierer..
// Initialisiere das Modell und den Optimierer
auto net = std::make_shared<Net>();
auto opt = torch::optim::AdamOptions(1e-4);
auto optimizer = torch::optim::Adam(net->parameters(), opt);
Generierung der Trainingsdaten
Hier generieren wir die Trainingsdaten. Das Intervall0 bis \(2\, \pi\) enthält die x-Werte, und wir berechnen die Zielwerte als Sinusfunktion dieser Datenpunkte.
// Generiere Trainingsdaten
auto x = torch::linspace(0, 2 * M_PI, 512).reshape({-1, 1});
auto target = torch::sin(x);
x.set_requires_grad(true);
Trainingsschleife
Der Hauptteil des Programms ist die Trainingsschleife, in der das Modell über mehrere tausend Iterationsschritte (Epochen) hinweg trainiert wird. Wir werten das aktuelle Modell über net->forward(x) aus, berechnen die Verlustfunktion und führen anschließend den Optimierungsschritt durch.
net->train();
for (size_t epoch = 0; epoch < optiSteps; ++epoch) {
auto predictions = net->forward(x);
auto loss = loss_function_period(predictions, target, x, net);
const double loss_value = loss.item<double>();
loss.backward();
optimizer.step();
optimizer.zero_grad();
if (epoch % 100 == 0)
cout << "Epoch [" << epoch << "], Loss: " << loss_value << endl;
if (fabs(loss_value) < tol)
{
cout << " loss < tol : " << loss_value;
cout << " STOP optimization-loop. " << endl;
break;
}
}
Modellspeicherung
Am Ende des Programms speichern wir das trainierte Modell. Die Speicherung des Modells erfolgt mit torch::save(net, "trained_model.pt"). Das PT-Format (PyTorch-Format) enthält alle notwendigen Informationen, um das neuronale Netzwerk später wieder zu laden und auszuwerten. Dieses Format ist plattformunabhängig und ermöglicht es, das Modell auf verschiedenen Geräten oder in unterschiedlichen Umgebungen wiederherzustellen, wenn die Netzwerkstruktur bekannt ist.
// Modell speichern
std::cout << " save model " << std::endl;
torch::save(net, "trained_model.pt");
return EXIT_SUCCESS;
}
Verlustfunktionen
Das Programm verwendet zwei Verlustfunktionen. Die erste ist der Standard-Fehler (Mean Squared Error), der zur Berechnung des Fehlers zwischen den Vorhersagen und den Zielwerten dient.
torch::Tensor loss_function(const torch::Tensor &predictions,
const torch::Tensor &targets) {
// Mean Squared Error
return torch::mse_loss(predictions, targets);
}
$$
\mathcal{L}_{\text{standard}} = \frac{1}{N} \sum_{i=1}^{N} (y_i – \hat{y}_i)^2
$$
wobei:
- \( y_i \) die Zielwerte (targets) sind,
- \( \hat{y}_i \) die Vorhersagen (predictions) des Modells sind,
- \( N \) die Anzahl der Datenpunkte ist.
Periodizitätsverlust
Die zweite Verlustfunktion enthält neben der Standard-Fehler-Komponente auch eine Periodizitäts-komponente. Durch Verschieben der Eingaben um Vielfache von \(2 \, \pi\) und Berechnung des Fehlers zwischen den verschobenen Vorhersagen und den ursprünglichen Vorhersagen wird das Netzwerk gezwungen, die periodische Natur der Sinusfunktion zu lernen (das vergrößert im Prinzip das Trainingsintervall).
$$
\mathcal{L}_{\text{total}} = \mathcal{L}_{\text{standard}} + \lambda \; \mathcal{L}_{\text{periodic}}
$$
wobei der Periodizitätsverlust definiert ist als:
$$
\mathcal{L}_{\text{periodic}} = \frac{1}{2K} \sum_{k=-K, k \neq 0}^{K} \frac{1}{N} \sum_{i=1}^{N} \left(\hat{y}(x_i + k \cdot 2\pi) – \hat{y}_i\right)^2
$$
Hierbei:
- \(\mathcal{L}_{\text{standard}}\) ist der Standard-Fehler (Mean Squared Error).
- \(\mathcal{L}_{\text{periodic}}\) ist der Periodizitätsfehler.
- \(\lambda\) ist der Gewichtungsfaktor für die Periodizitätskomponente.
- \(K\) ist die Anzahl der Periodenverschiebungen.
- \(N\) ist die Anzahl der Datenpunkte.
- \(\hat{y}(x_i + k \cdot 2\pi)\) sind die Vorhersagen für die um \(k \cdot 2\pi\) verschobenen Eingaben \(x_i\).
- \(\hat{y}_i\) sind die ursprünglichen Vorhersagen des Modells.
torch::Tensor loss_function_period(const torch::Tensor &predictions,
const torch::Tensor &targets,
torch::Tensor inputs,
shared_ptr<Net>& net)
{
// Mean Squared Error
auto standard_loss = torch::mse_loss(predictions, targets);
const int K = 2;
const double lambda_periodicity = 1.0;
// Periodicity loss
torch::Tensor periodicity_loss = torch::zeros({1}, torch::kFloat);
for (int k = -K; k <= K; ++k) { if (k != 0) {
auto shifted_inputs = inputs + k * 2 * M_PI;
auto shifted_predictions = net->forward(shifted_inputs);
periodicity_loss += torch::mse_loss(shifted_predictions, predictions);
}
}
// Total loss
auto total_loss = standard_loss + lambda_periodicity * 1..0/(2.0*K) * periodicity_loss;
return total_loss;
}
Netzwerkstruktur
Das neuronale Netzwerk besteht aus mehreren voll verbundenen Schichten.
#include "tools.h"
// Definiere das Modell
struct Net : torch::nn::Module {
Net() {
// Baue das Netz mit 2 versteckten Schichten
const int N=10;
fc1 = register_module("fc1" , torch::nn::Linear(1, N));
fc2 = register_module("fc2" , torch::nn::Linear(N, N));
fc3 = register_module("fc3" , torch::nn::Linear(N, N));
fc4 = register_module("fc4" , torch::nn::Linear(N, 1));
}
// Implementiere die Vorwaertsfunktion
torch::Tensor forward(const torch::Tensor &x) {
torch::Tensor y = fc1->forward(x);
y = torch::tanh(fc2->forward(y));
y = torch::tanh(fc3->forward(y));
y = fc4->forward(y);
return y;
}
torch::nn::Linear fc1{nullptr}, fc2{nullptr}, fc3{nullptr}, fc4{nullptr};
};
Das Netzwerk besteht aus vier vollständig verbundenen Schichten:
- fc1: Die erste Schicht ist eine lineare Schicht, die einen Eingabewert auf \( N \) Neuronen abbildet.
- fc2: Die zweite Schicht ist ebenfalls eine lineare Schicht, die die \( N \) Neuronen der ersten Schicht auf \( N \) Neuronen abbildet und die Tanh-Aktivierungsfunktion verwendet.
- fc3: Die dritte Schicht ist eine weitere lineare Schicht, die die \( N \) Neuronen der zweiten Schicht auf \( N \) Neuronen abbildet und ebenfalls die Tanh-Aktivierungsfunktion verwendet.
- fc4: Die vierte Schicht ist eine lineare Schicht, die die \( N \) Neuronen der dritten Schicht auf einen einzelnen Ausgabewert abbildet.
Die Vorwärtsfunktion torch::Tensor forward(const torch::Tensor &x) leitet die Eingabedaten durch die verschiedenen Schichten des Netzwerks. In der ersten Schicht verwenden wir keine Aktivierungsfunktion. In der zweiten und dritten Schicht setzen wir Tanh-Aktivierungsfunktionen ein.
Weitere Möglichkeiten für Aktivierungsfunktionen
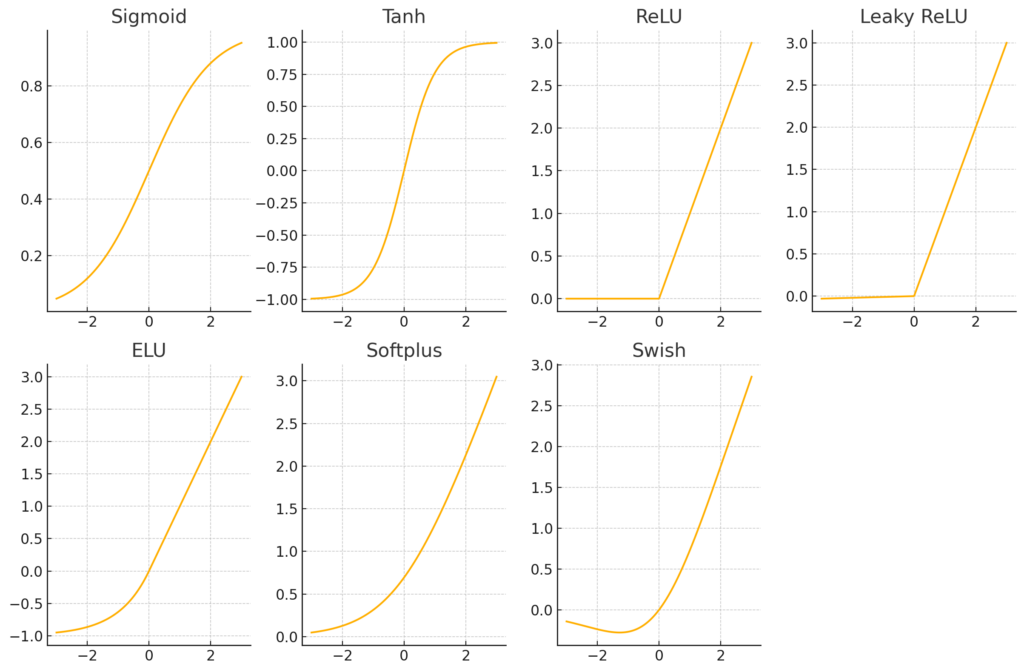
Neben Sigmoid und Tanh
\[
\text{Sigmoid}(x) = \sigma(x) = \frac{1}{1 + \exp(-x)}, \qquad \tanh(x) = \frac{\sinh(x)}{\cosh(x)} = \frac{e^x – e^{-x}}{e^x + e^{-x}}
\]
gibt es weitere gängige Aktivierungsfunktionen, die üblicherweise in neuronalen Netzwerken verwendet werden:
- ReLU (Rectified Linear Unit): \( \text{ReLU}(x) = \max(0, x) \)
- Leaky ReLU: \( \text{Leaky ReLU}(x) = \max(0.01x, x) \)
- ELU (Exponential Linear Unit): \( \text{ELU}(x) = \begin{cases}
x & \text{if } x > 0 \\
\alpha (\exp(x) – 1) & \text{if } x \leq 0
\end{cases} \) - Softplus: \( \text{Softplus}(x) = \log(1 + \exp(x)) \)
- Swish: \( \text{Swish}(x) = x \cdot \sigma(x) \), wobei \( \sigma(x) \) die Sigmoid-Funktion ist.
Jede dieser Aktivierungsfunktionen hat ihre eigenen Vor- und Nachteile und kann je nach spezifischer Anwendung und Daten unterschiedliche Ergebnisse liefern. Die Wahl der Aktivierungsfunktion kann einen erheblichen Einfluss auf die Leistung eines neuronalen Netzwerks haben.
Inference des neuronalen Netzwerks, Programm evaluate
Inference ist der Prozess, bei dem das trainierte Modell auf neue Daten angewendet wird, um Vorhersagen zu generieren.
Das Programm evaluate lädt das zuvor trainierte Modell und generiert Testdaten im Bereich von \(0, 2 \, \pi\) (standardmäßig) oder in einem benutzerdefinierten Bereich, die dann Eingangsdaten des neuronalen Netzwerks sind. Die Testdaten werden durch das neuronale Netzwerk geleitet, welches daraus die Ausgabedaten erzeugt. Der Fehler zwischen den Vorhersagen und den wahren Werten (Sinusfunktion) wird berechnet und in eine Datei ausgegeben.
Der erste Block des Programms beinhaltet die notwendigen Bibliotheken, Definitionen und das Laden des trainierten Modells. Es ist wichtig, dass die Netzwerkarchitektur (die Klasse Net) genau die gleiche Struktur hat wie beim Training, damit die gespeicherten Daten (trained_model.pt) korrekt geladen werden können.
#include <iostream>
#include <torch/torch.h>
#include <iostream>
#include <fstream>
#include "net.h"
// Beschreibung der Argumente:
// ---------------------------
// 1. B (optional): Der Bereich der Eingabewerte fuer die Testdaten, Standardwert: 4pi
//
int main(int argc, char *argv[]) {
// Modell laden
auto net = std::make_shared<Net>();
torch::load(net, "trained_model.pt");
Als nächstes initialisiert das Programm die Testdaten und wertet das neuronale Netzwerk mit net->forward(test_x) aus.
float A = 0.0;
float B = 2*M_PI;
if (argc == 2)
B = atof(argv[1]);
// Teste das Modell
net->eval();
auto test_x = torch::linspace(0, B, 200).reshape({-1, 1});
auto test_y = net->forward(test_x); // Inference
auto solution = torch::sin(test_x);
auto error = test_y - torch::sin(test_x);
auto e = torch::norm(error, 2).item<float>();
std::cout << std::setprecision(9);
std::cout << "Test predictions error : " << e << std::endl;
Dieser Block extrahiert die Vorhersagen und speichert sie zusammen mit den Eingabewerten in eine Datei.
// Extrahieren der Komponenten in einen std::vector
const int nx = test_x.numel();
const int ny = test_y.numel();
std::vector<float> X(test_x.data_ptr<float>(), test_x.data_ptr<float>() + nx);
std::vector<float> Y(test_y.data_ptr<float>(), test_y.data_ptr<float>() + ny);
std::ofstream data("data.txt");
for (uint i = 0; i < X.size(); ++i)
data << X[i] << " " << Y[i] << std::endl;
data.close();
return EXIT_SUCCESS;
}
Die Testrechnungen für die PINNs sind unter diesem Link verfügbar.
Quellen
- (2019): PyTorch: An Imperative Style, High-Performance Deep Learning Library. In: Advances in Neural Information Processing Systems 32, S. 8024–8035, Curran Associates, Inc., 2019.
- (2024): Can AI Solve Science?. https://writings.stephenwolfram.com/2024/03/can-ai-solve-science, 2024, (Accessed: 2024-07-11).