Testrechnungen PINNs

Hier werden die Ergebnisse der Testrechnungen für das PINNs: Physics-Informed Neural Network dargestellt und kurz analysiert. Der Schwerpunkt liegt auf dem Verhalten der PINNs außerhalb des Trainingsintervalls sowie dem Frequenz-Prinzip (F-Prinzip), das beschreibt, wie neuronale Netze unterschiedliche Frequenzen lernen – insbesondere, dass niedrige Frequenzen schneller erfasst werden als hohe.

„Ich mache nie Voraussagen und werde das auch niemals tun.“
— Paul Gascoigne^[1]

Ergebnisse der PINN-Auswertung, Programm evaluate

Die Testdaten wurden im Bereich von $0$ bis $2\pi$ generiert, also mit dem Trainingsintervall übereinstimmend.
$$
x_i = \frac{i \, 2 \pi}{N}, \qquad i=0,\ldots, N .
$$
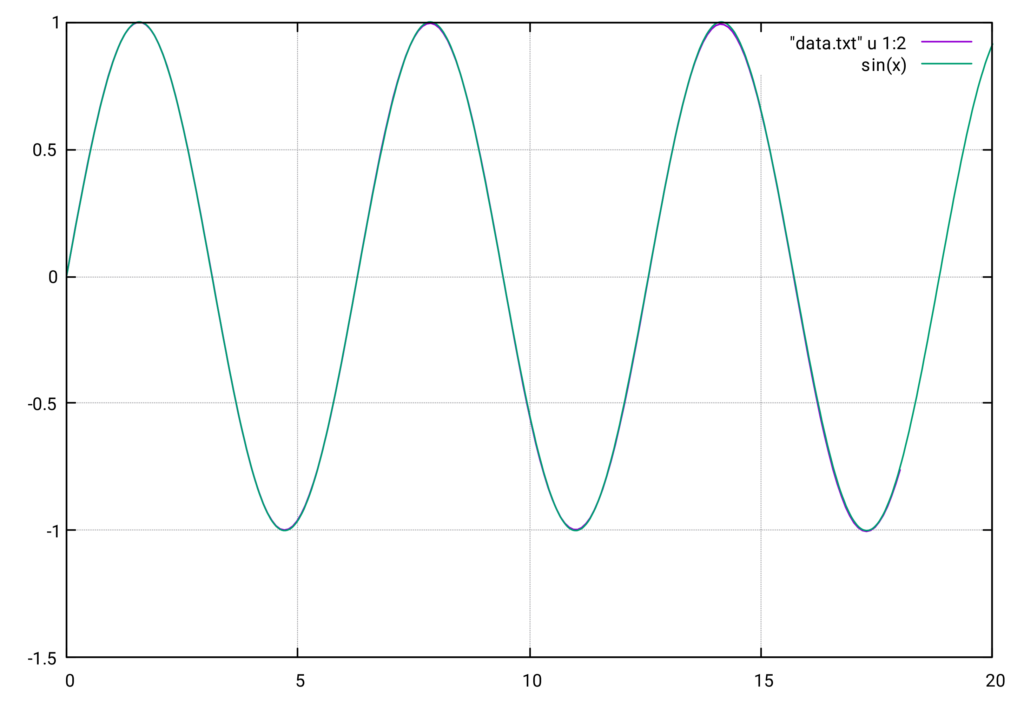
Das folgende Diagramm zeigt die Auswertung des PINN ( net->forward(x) ) im Vergleich zur tatsächlichen $\sin(x)$-Funktion.

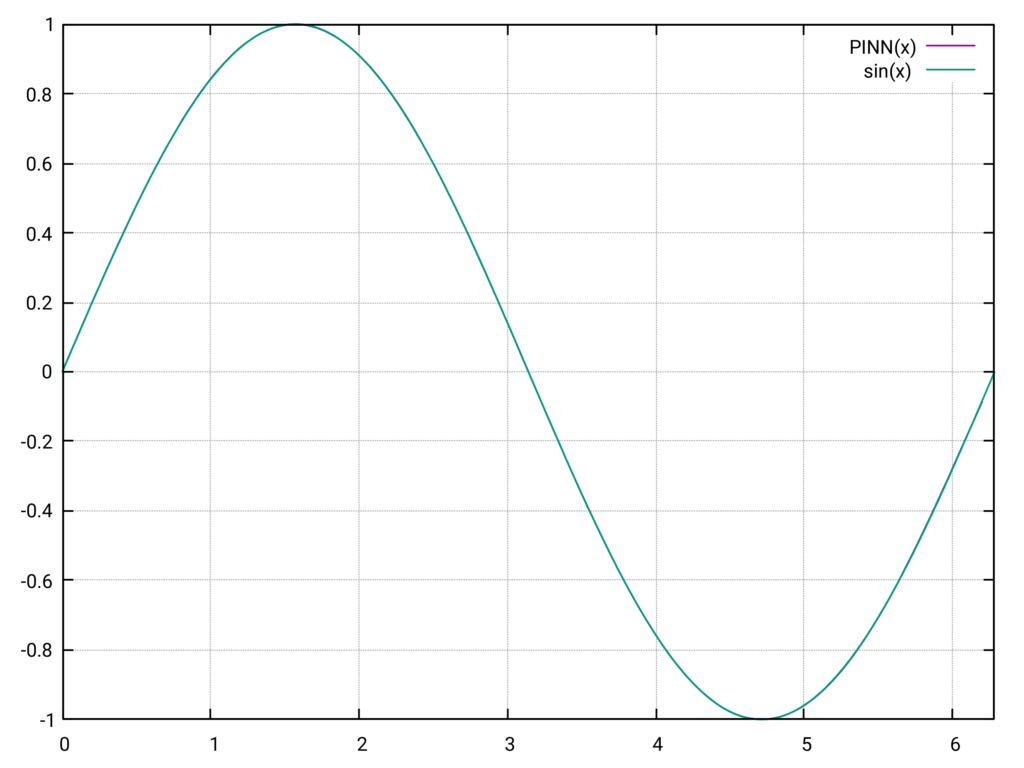
Testrechnungen PINNs : Auswertung — Auswertung des PINN im Vergleich zur sin-Funktion

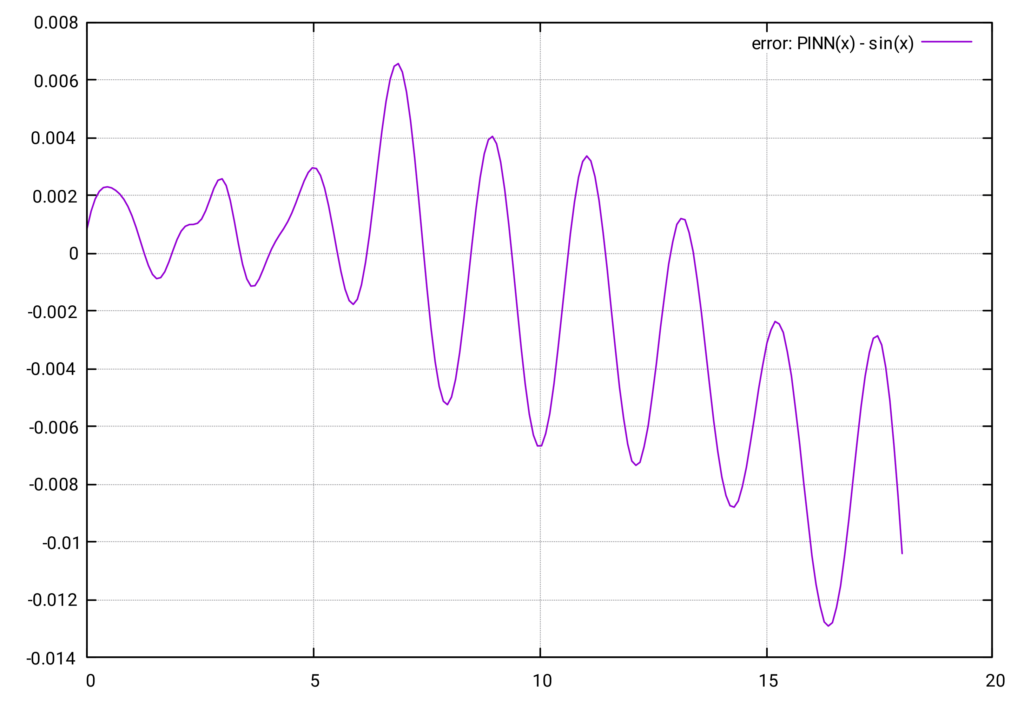
Die beiden Kurven liegen praktisch übereinander, der Fehler ist von der Größenordnung $\mathcal{O}(10^{-3})$. Das ist eine bemerkenswert präzise Approximation der $\sin(x)$-Funktion. Allerdings ist gegen Ende des Intervalls eine leichte Zunahme des Fehlers zu beobachten.

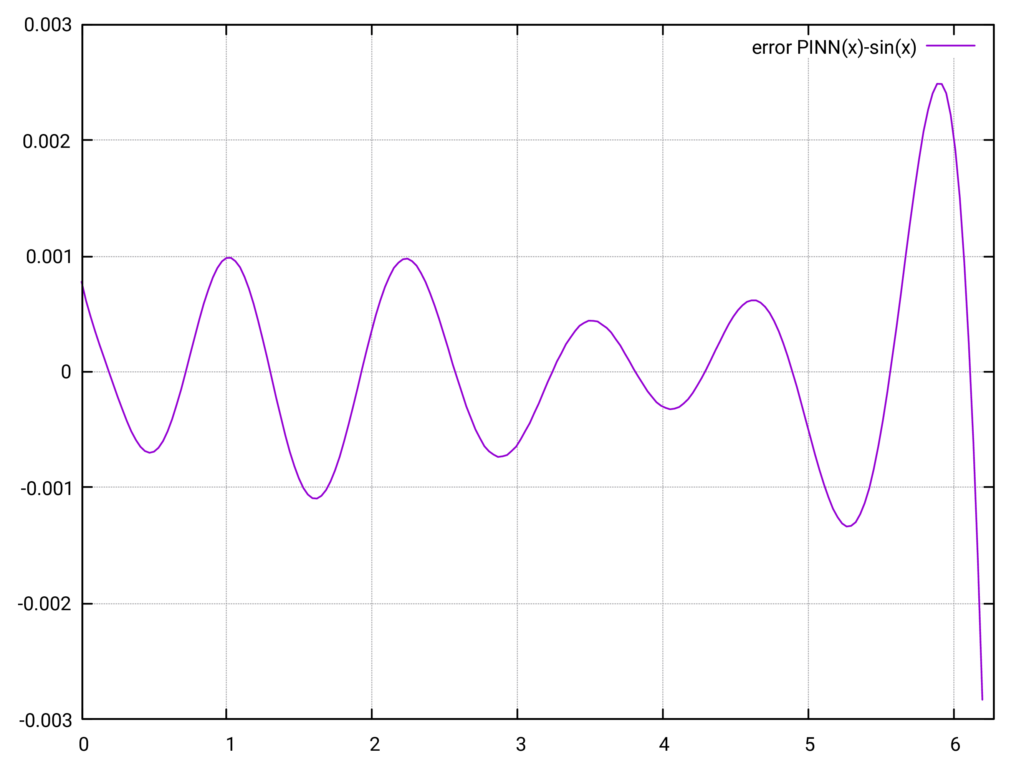
Testrechnungen PINNs : Fehler (PINN(x) - sin(x))-Funktion — Fehler PINN(x) – sin(x)

Auswertung über das Trainingsintervall hinaus

Die folgende Auswertung zeigt das Verhalten des PINN außerhalb des Trainingsintervalls $0$ bis $2\pi$. Wie in den Diagrammen zu sehen ist, nimmt der Fehler außerhalb des Trainingsintervalls stark zu, was die Verwendung des PINN für $x > 2\pi$ unbrauchbar macht. Es sieht so aus, als folge der Funktionsverlauf der Aktivierungsfunktion $\tanh$.

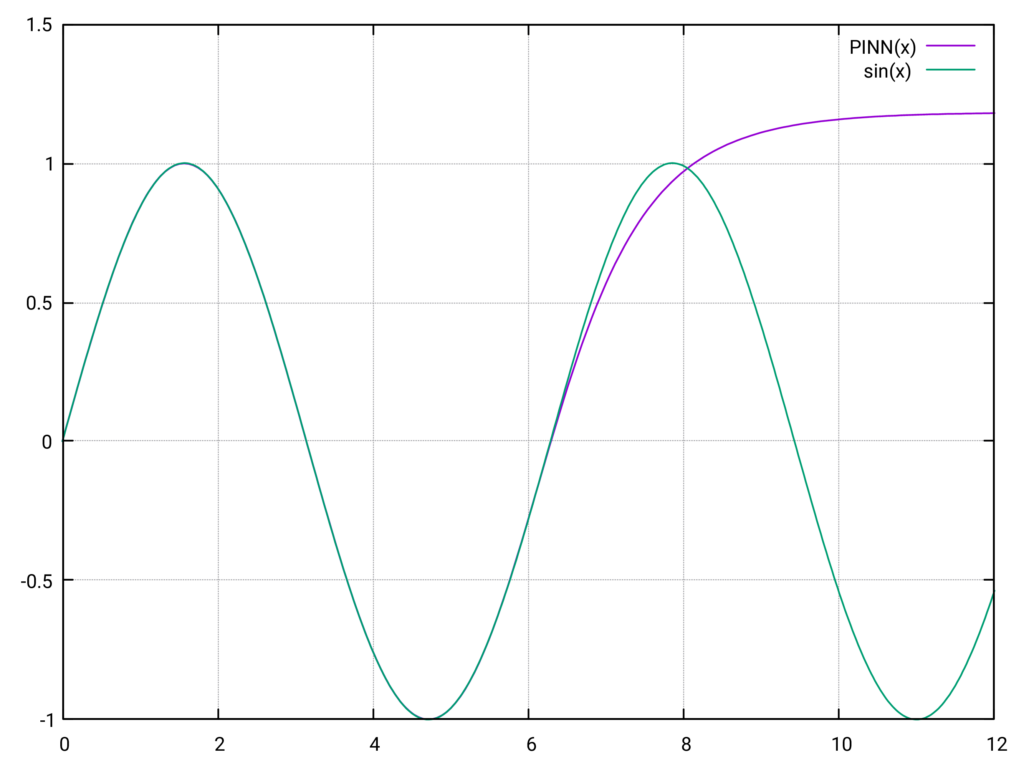
Testrechnungen PINNs Auswertung des PINN im Vergleich zur (sin(x))-Funktion außerhalb des Trainingsintervalls — Auswertung des PINN im Vergleich zur sin-Funktion außerhalb des Trainingsintervalls $ [0, 2\pi] $

Der Fehler des PINN außerhalb des Trainingsintervalls ist von der Größenordnung $\mathcal{O}(1)$.

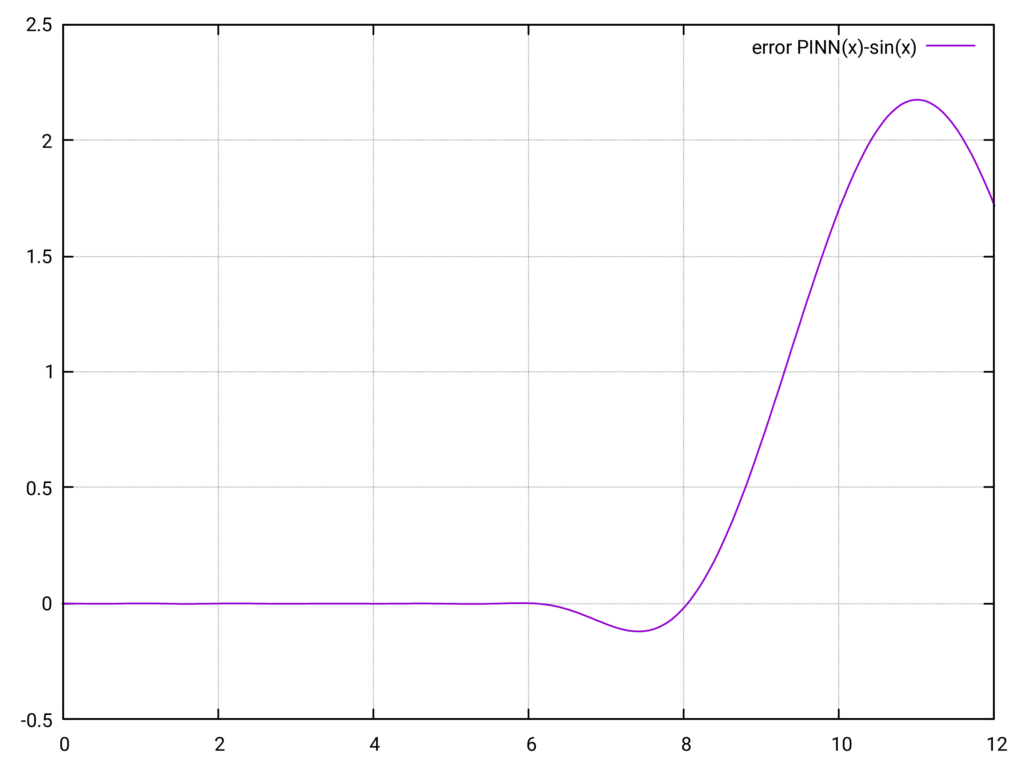
Testrechnungen PINNs Fehler e(x) = PINN - sin(x) — Fehler e(x) = PINN(x) – sin(x) für $x \in (0,12) $.

Training mit Berücksichtigung der Periodizität

Wir fügen nun Wissen über die gesuchte Funktion hinzu und fordern Periodizität. Dies führt zur Erweiterung des Funktionals:

$$
\mathcal{L}_{\text{total}} = \mathcal{L}_{\text{standard}} + \frac{1}{2K} \sum_{k=1}^{K} \frac{1}{N} \sum_{i=1}^{N} \left(\hat{y}(x_i + k \cdot 2\pi) – \hat{y}_i\right)^2
$$

Mit dem Wert $ K=2 $ sind die Trainingsdaten aus dem Bereich $I = [0, 6\pi]$. Die Approximation ist in $ I $ wieder sehr gut.

Testrechnungen PINNs — PINN trainiert mit $\mathcal{L}_{\text{standard}} + \lambda \; \mathcal{L}_{\text{periodic}}$

Sobald allerdings das Intervall verlassen wird, steigt der Fehler stark an und die PINN-Funktion wird wieder unbrauchbar.

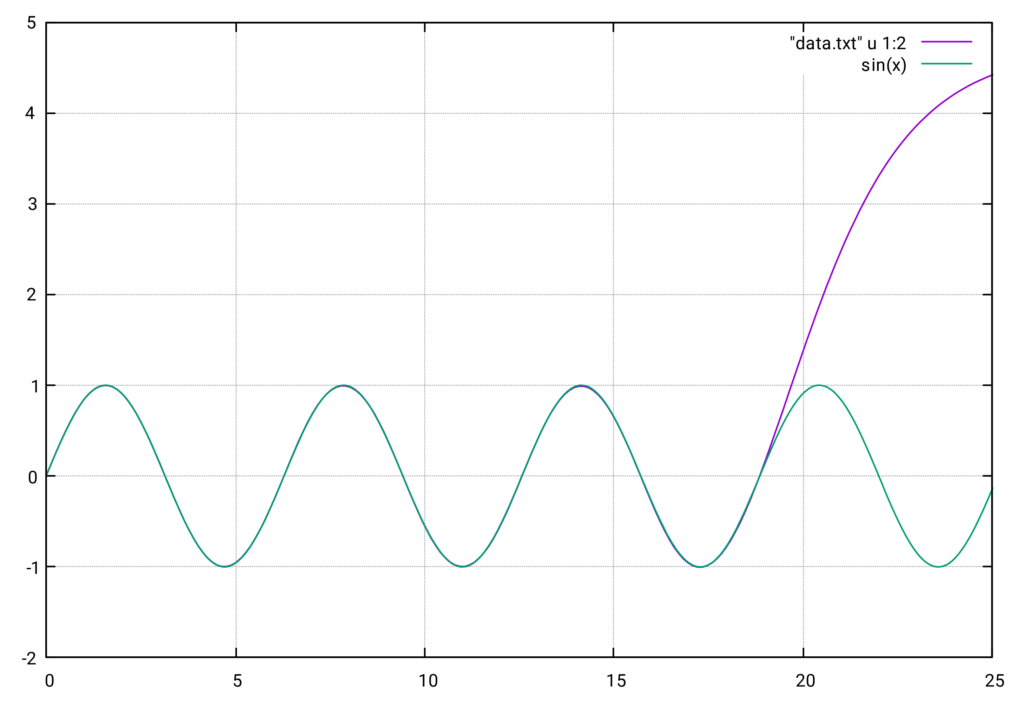
Der Ausweg ist hier ein alternativer Ansatz mit einem LSTM-Modell, der dieses Problem erfolgreich meisterte. Das Modell erkannte die periodische Struktur des Signals und extrapolierte es zuverlässig. Details und Ergebnisse finden sich im Beitrag Zeitreihenanalyse mit LSTM.

Frequenz-Prinzip

Das Frequenz-Prinzip ^[1]^[2]^[3] (auch F-Prinzip) besagt, dass neuronale Netze dazu neigen, niederfrequente Komponenten eines Signals schneller zu lernen als hochfrequente Komponenten. Das bedeutet, dass während des Trainings die glatten, langsamen Veränderungen im Signal zuerst erfasst werden, während die detaillierteren, schnelleren Veränderungen länger dauern. Genau das beobachten wir auch, wenn wir statt $\sin⁡(x)$ die höherfrequenten Funktionen $\sin⁡(k \, x)$ mit $k=2,3,4,8$ approximieren. Das Training benötigt mehr Iterationsschritte, je größer $k$ ist.

Funktion	Iterationen bis $ \text{Verlust} < 10^{-5} $
$\sin(x)$	10 200
$\sin(2x)$	10 900
$\sin(3x)$	41 200
$\sin(4x)$	51 600
$\sin(8x)$	> 100 000

Die folgende Grafik zeigt den typischen Verlauf des Trainingsverlusts für verschiedene Werte von $k$. Je höher die Frequenz, desto langsamer verläuft die Konvergenz.

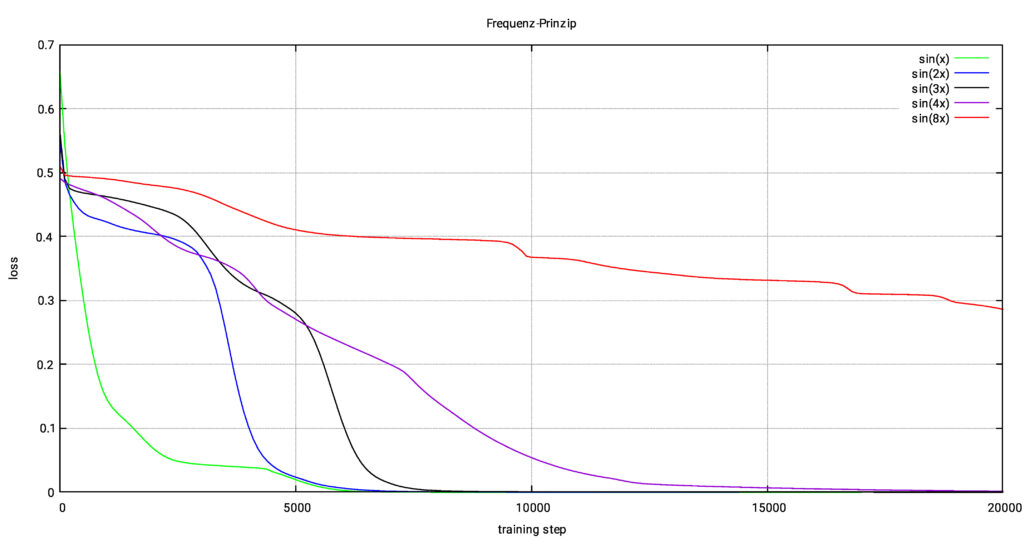
Frequenz-Prinzip bei Sinusfunktionen: Trainingsverlauf des Verlusts — Trainingsverlauf des Verlusts ($\text{loss}$) beim Erlernen von $\sin(kx)$ für verschiedene Frequenzen $k$.

Interessanterweise spiegelt dieses Verhalten das der Mehrgitterverfahren wider. Dort wird die Grobgitterkorrektur eingeführt, um die klassischen Iterationsverfahren, die gerade die hochfrequenten Komponenten gut erfassen, zu ergänzen, da diese bei den niedrigfrequenten Anteilen Schwierigkeiten haben. Die Grobgitterkorrektur löst ein Ersatzproblem für die langsamen Anteile, würde aber für die hochfrequenten Komponenten keine Lösung finden. Das F-Prinzip beschreibt demnach das Verhalten der Grobgitterkorrektur. Für das Mehrgitterverfahren ergibt sich insgesamt durch die Kombination von klassischen Iterationsverfahren und Grobgitterkorrektur ein sehr effizientes Verfahren mit optimaler Konvergenzrate.

Die spannende Frage, die sich hier stellt, lautet: Wie könnte ein Glätter für neuronale Netze aussehen? Welche Ansätze könnten helfen, hochfrequente Komponenten effizienter zu lernen und so das Training von neuronalen Netzen, insbesondere PINNs, weiter zu optimieren?

Ich verwende dieses Zitat mit großem Respekt für Paul Gascoigne – einen außergewöhnlichen Fußballer, einen Ausnahmespieler, der mit Talent, Verletzlichkeit und Offenheit viele Menschen berührt und beeindruckt hat. ↩︎

Quellen

Zhi-Qin John Xu and Yaoyu Zhang and Tianwei Luo and Yanyang Xiao and Zheng Ma and Zhihua Wen (2019): Frequency Principle: Fourier Analysis Sheds Light on Deep Neural Networks. In: arXiv preprint arXiv:1901.06523, 2019.
Lu Lu and Pengzhan Jin and Guofei Pang and Zhongqiang Zhang and George Em Karniadakis (2021): Learning nonlinear operators via DeepONet based on the universal approximation theorem of operators. In: Nature Machine Intelligence, Bd. 3, Nr. 3, S. 218–229, 2021.
Tao Luo and Zheng Ma and Zhi-Qin John Xu and Yaoyu Zhang (2019): Theory of the Frequency Principle for General Deep Neural Networks. 2019.