In diesem Beitrag möchte ich erste Resultate aus der Implementierung und Anwendung eines Long Short-Term Memory (LSTM)-Netzwerks in C++ mit der libtorch-Bibliothek vorstellen. Ziel war es, die Leistungsfähigkeit eines LSTM-Modells für Zeitreihenanalysen, insbesondere bei der Vorhersage eines verrauschten Sinus-Signals, zu untersuchen. Das LSTM-Modell hat dabei gezeigt, wie effektiv es Muster in Daten erkennen und extrapolieren kann.
Motivation
Zeitreihenanalysen sind ein zentraler Bestandteil vieler Anwendungen, von der Anomalieerkennung in Sensordaten bis zur Vorhersage von Wetterdaten oder Aktienkursen. Python mit Bibliotheken wie PyTorch wird häufig für die Entwicklung solcher Modelle verwendet. Jedoch kann C++ mit libtorch in Szenarien mit hohen Anforderungen an Performance und Integration von Vorteil sein, insbesondere wenn es um Echtzeitanwendungen geht.
Ein interessanter Vergleich ergibt sich hier zur Anwendung von Physics-Informed Neural Networks (PINNs). Wie in diesem Beitrag beschrieben, zeigte sich, dass ein forward PINN bei der Modellierung eines Sinus-Signals außerhalb des Trainingsintervalls nicht erfolgreich war. Deshalb wurde ein LSTM-Modell eingesetzt, das sich als besonders geeignet für diese Aufgabe erwies. Im Kern handelt es sich hierbei um Mustererkennung, wobei das Muster die periodische Struktur des Sinus ist.
Der mathematische Hintergrund sowie die Funktionsweise der LSTM und die Rolle der Sequenzen werden in einem späteren Beitrag detailliert beschrieben. Weitere Informationen zu den LSTM-Modellen finden sich hier.
Programmblöcke und Funktionsweise
Das Programm zur Zeitreihenanalyse mit LSTM in C++ ist modular aufgebaut. Es umfasst folgende Schritte:
1. Header und Bibliotheken
Zu Beginn werden notwendige Bibliotheken eingebunden, die die grundlegende Funktionalität bereitstellen:
#include "net.h"
#include <vector>
#include <cmath>
#include <fstream>
#include <algorithm>
#include <string>
#include <torch/torch.h>
Die Programmstruktur basiert auf einem LSTM-Modell, das in einer eigenen Klasse definiert ist. Es enthält eine LSTM-Schicht und eine vollständig verbundene Schicht, die die Ausgabe erzeugt. Der folgende Codeauszug zeigt die zentrale Struktur:
#ifndef NET_H
#define NET_H
#include <torch/torch.h>
#include <iostream>
// Definition des LSTM-Modells
struct LSTMModel : torch::nn::Module {
LSTMModel(int64_t input_size, int64_t hidden_size, int64_t output_size)
: lstm(torch::nn::LSTMOptions(input_size, hidden_size).batch_first(true)),
fc(hidden_size, output_size) {
register_module("lstm", lstm);
register_module("fc", fc);
}
torch::Tensor forward(torch::Tensor x) {
auto lstm_out = lstm->forward(x);
auto last_hidden = std::get<0>(lstm_out).select(1, -1); // Letzter Zeitschritt
return fc->forward(last_hidden);
}
torch::nn::LSTM lstm{nullptr};
torch::nn::Linear fc{nullptr};
};
#endif // NET_H
2. Generierung und Verarbeitung der Zeitreihe
Die Funktion generate_time_series erzeugt eine Sinusfunktion mit zufälligem Rauschen. Für die Vorbereitung der Daten werden zwei Funktionen verwendet:
- Normalisierung: Die Werte der Zeitreihe werden in den Bereich [-1, 1] skaliert.
-
Sequenzen erstellen: Die Funktion
create_sequenceserstellt Eingabesequenzen (Features) und Zielwerte (Labels):
std::pair<torch::Tensor, torch::Tensor> create_sequences(const std::vector<double>& data, int seq_length) {
std::vector<torch::Tensor> inputs, targets;
for (size_t i = 0; i < data.size() - seq_length; ++i) {
auto seq = torch::tensor(std::vector<double>(data.begin() + i, data.begin() + i + seq_length), torch::kFloat32);
auto label = torch::tensor(data[i + seq_length], torch::kFloat32);
inputs.push_back(seq);
targets.push_back(label);
}
return {torch::stack(inputs), torch::stack(targets)};
}
3. Speicherung und Ausführung
Das LSTM-Modell besteht wird mit dem Adam-Optimizer trainiert, wobei der Verlust mit der Mean Squared Error (MSE) Funktion berechnet wird. Der Trainingsprozess verbessert iterativ die Modellparameter.
Nach dem Training werden das Modell und die Normalisierungsparameter gespeichert. Das Hauptprogramm kombiniert alle Schritte und überwacht den Fortschritt mit regelmäßigen Verlustausgaben:
int main() {
auto time_series = generate_time_series(500);
double min_val, max_val;
auto normalized_series = normalize(time_series, min_val, max_val);
auto [train_X, train_y] = create_sequences(normalized_series, 20);
auto model = std::make_shared<LSTMModel>(1, 50, 1);
torch::optim::Adam optimizer(model->parameters(), torch::optim::AdamOptions(0.001));
for (int epoch = 1; epoch <= 1000; ++epoch) { model->train();
optimizer.zero_grad();
auto output = model->forward(train_X.unsqueeze(-1));
auto loss = torch::mse_loss(output.squeeze(), train_y);
loss.backward();
optimizer.step();
if (epoch % 10 == 0) std::cout << "Epoch " << epoch << ", Loss: " << loss.item<double>() << "\\n";
}
torch::save(model, "lstm_sin_model.pt");
}
Beispielanwendung
Ein einfacher Sinusgenerator diente als Testfall. Das Ziel bestand darin, zukünftige Werte des Signals basierend auf vorherigen Werten vorherzusagen. Dazu wurden:
- Trainingsdaten mit einem Sinus-Signal über 1000 Schritte erzeugt.
- Störungen (Rauschen) hinzugefügt, um die Robustheit des Modells zu testen.
Resultate
- Das Modell konnte den Verlauf des Sinus-Signals nach wenigen Epochs mit relativ hoher Genauigkeit vorhersagen.
- Selbst bei moderatem Rauschen blieb die Vorhersage stabil, mit einer MSE von unter 0.001.
Die Trainingszeit für 1000 Epochs lag bei ca. 11 Sekunden auf einem Ryzen 9 5950X. Dabei wurden alle 16 Kerne genutzt.
Die folgende Abbildung zeigt die Trainingsdaten (lila) im Bereich [0, 50] und die Vorhersage des LSTM-Modells (grün) über das Trainingsintervall hinaus. Das Modell hat die periodische Struktur des Signals erfolgreich gelernt und extrapoliert.
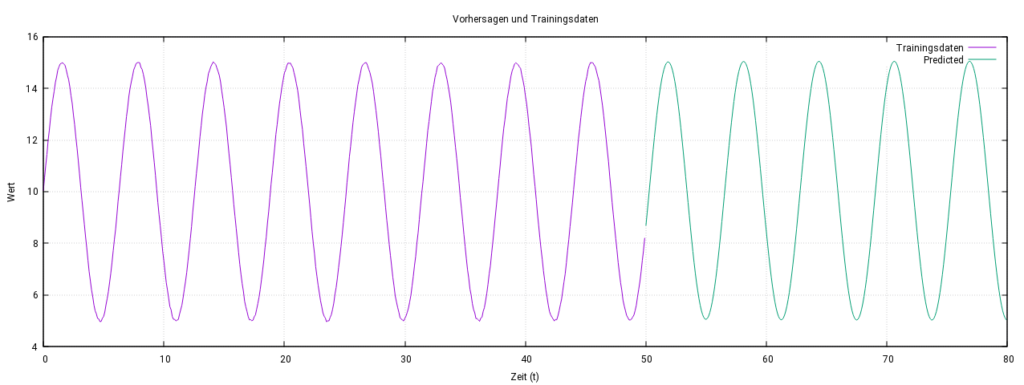
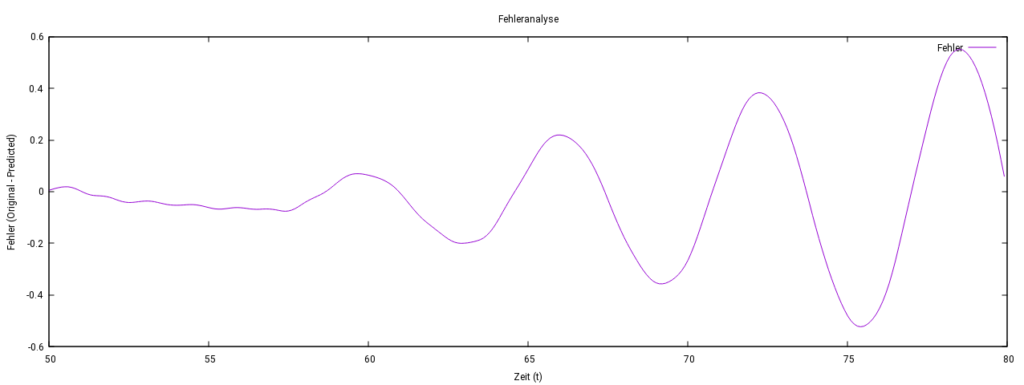
Das Modell sagte das Verhalten auch über das Trainingsintervall [0,50] hinaus erfolgreich vorher. Es erkannte die periodische Struktur des Signals, indem es zeitliche Muster in den Eingabedaten analysierte. Die Gewichtsmuster in der LSTM-Schicht ermöglichten es, wiederkehrende Muster im Signal zu lernen und zuverlässig zu reproduzieren, auch außerhalb des Trainingsintervalls. Allerdings wuchs der Fehler mit zunehmender Entfernung vom Trainingsintervall, blieb jedoch insgesamt kleiner als 3,5 %.
Vorhersage verrauschter Sinus-Daten
Die vorliegenden Abbildungen zeigen die Ergebnisse eines LSTM-Modells bei der Vorhersage schwach verrauschter Sinus-Daten. Trotz dieser Störungen lag der relative Fehler der Vorhersage durchgehend unter 3 %.
Die erste Abbildung zeigt die verrauschten Trainingsdaten (lila) und die Vorhersagen des LSTM-Modells (grün). Die zweite Abbildung analysiert den relativen Fehler über den gesamten Vorhersagezeitraum.
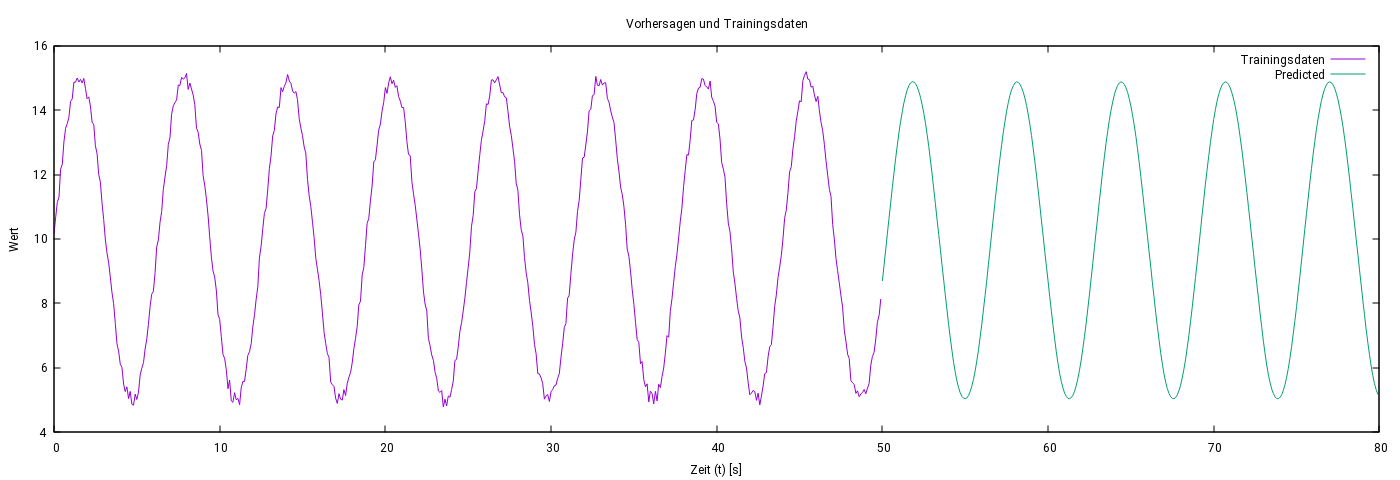
Abbildung 3: Vergleich von verrauschten Trainingsdaten (lila) und Vorhersagen (grün) des LSTM-Modells.
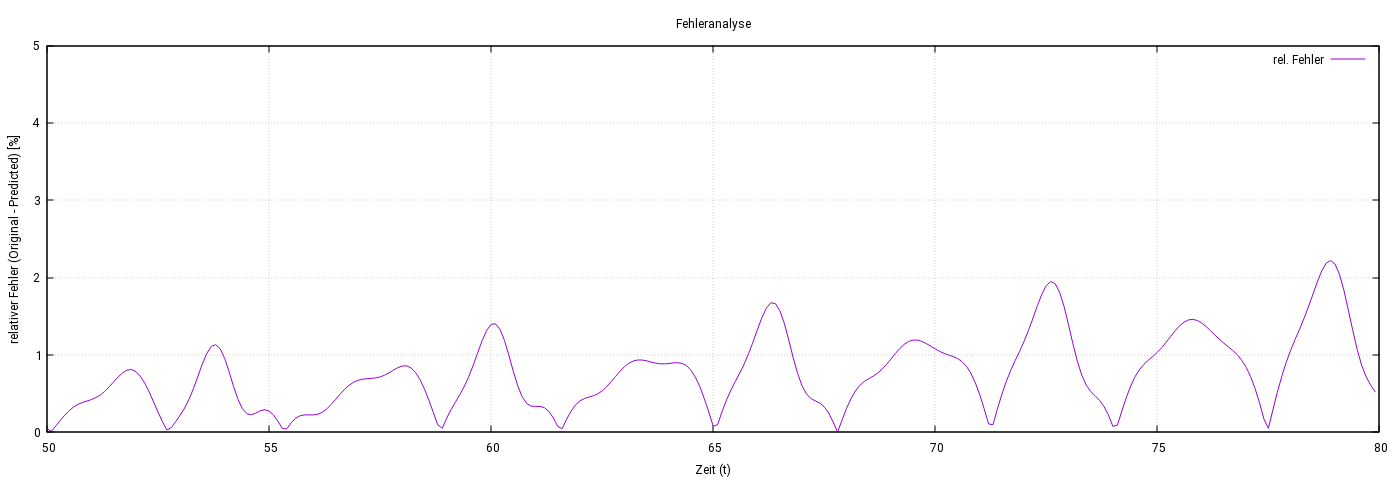
Abbildung 4: Relativer Fehler der Vorhersagen des LSTM-Modells: Der Fehler bleibt durchgehend unter 3 %.
Vorhersage bei starker Störung: Die Abb. 5 und Abb.6 zeigen die Ergebnisse eines LSTM-Modells bei der Vorhersage stark verrauschter Sinus-Daten, bei denen die Störung bis zu 20 % des Ausgangssignals beträgt. Trotz der starken Störungen konnte das Modell die Struktur des Signals innerhalb des Trainingsintervalls zuverlässig rekonstruieren. Außerhalb des Trainingsintervalls blieb der relative Fehler unter 10 %.
Die erste Abbildung zeigt die verrauschten Trainingsdaten (lila) und die Vorhersagen des LSTM-Modells (grün). Die zweite Abbildung stellt den relativen Fehler über den gesamten Vorhersagezeitraum dar.
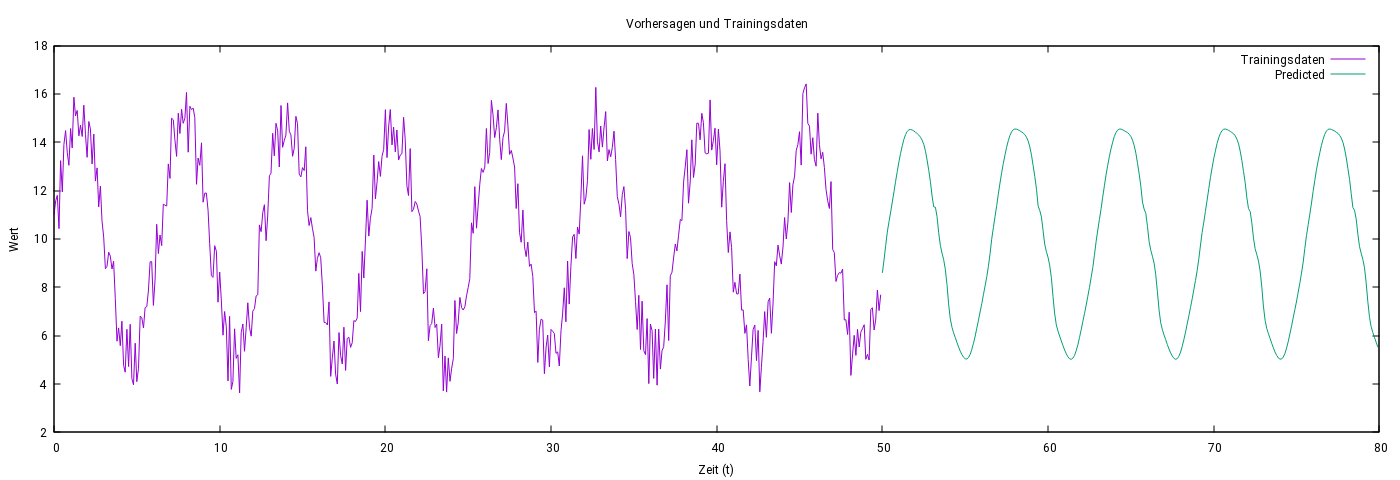
Abbildung 5: Vergleich von stärker verrauschten Trainingsdaten (lila) und Vorhersagen (grün) des LSTM-Modells.
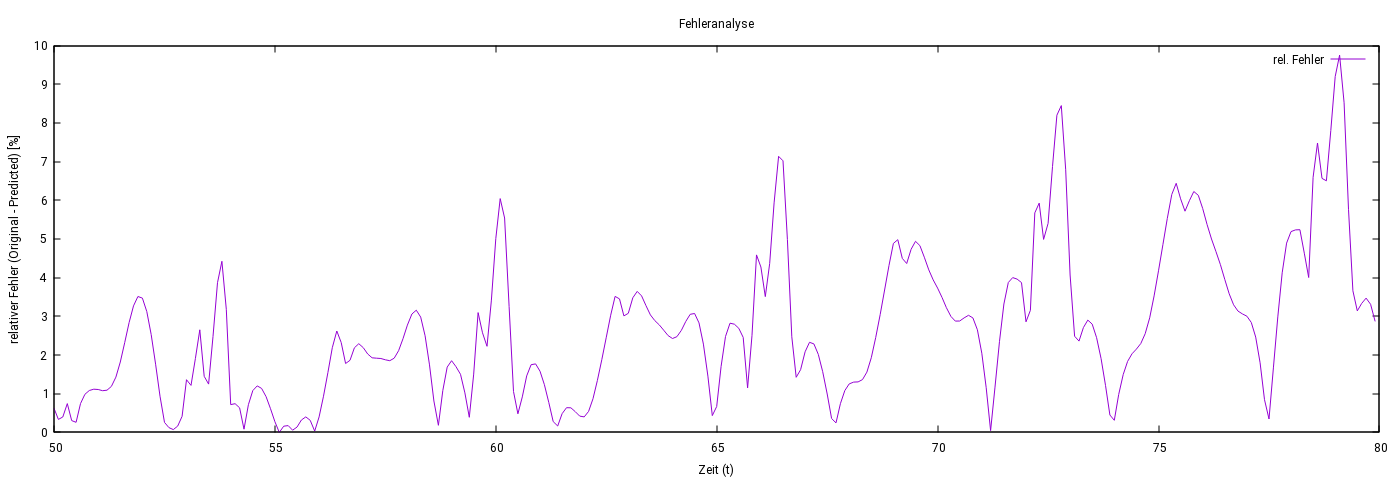
Abbildung 6: Relativer Fehler der Vorhersagen des LSTM-Modells: Der Fehler bleibt außerhalb des Trainingsintervalls unter 10 %, nimmt jedoch mit zunehmender Entfernung vom Trainingsintervall zu.
Fazit
Besonders hervorzuheben ist, dass das LSTM-Modell dort erfolgreich war, wo ein forward PINN beim Sinus-Signal versagte, und somit eine effektive Lösung für diese Klasse von Problemen bietet. Es handelt sich hierbei jedoch um ein sehr einfaches Beispiel, und das LSTM-Modell wurde ad hoc gewählt. Viele Fragen bleiben noch offen, wie etwa die optimale Anzahl der Schichten, die Länge der Sequenzen und mögliche Anpassungen des Modells für komplexere Anwendungen.