Nachfolgend beschreibe ich die Entwicklung einer Gewächshaussimulation mithilfe eines OpenFOAM-Modells, das insbesondere den Feuchtetransport berücksichtigt. Das Hauptziel ist es, ein Simulationswerkzeug bereitzustellen, das es den Benutzern ermöglicht, das Klima im Gewächshaus zu modellieren und zu analysieren.
Ziele
- Entwicklung eines OpenFoam-Modells, das die Strömung von Luft und die Transportprozesse von Feuchtigkeit im Gewächshaus gekoppelt simuliert.
- Vorhersage des Gewächshausklimas: Durch die Integration von Feuchtigkeitsmodellen in das Strömungsmodell sollen Vorhersagen über Temperatur, Luftfeuchtigkeit und Luftströmung im Gewächshaus ermöglicht werden. Dies ist entscheidend für die Optimierung von Wachstumsbedingungen und den Schutz der Pflanzen vor extremen Bedingungen.
Feuchtigkeit
Wasserdampf ist Wasser im gasförmigen Aggregatzustand. Nebel- bzw. Wassertröpfchen sind nicht Bestandteil des Wasserdampfes. Die Luftfeuchtigkeit (humidity) – oder kurz Luftfeuchte – bezeichnet den Anteil des Wasserdampfs am Gasgemisch der Luft. Flüssiges Wasser, zum Beispiel Regentropfen, Nebeltröpfchen oder Eis, etwa in Form von Schneekristallen, werden der Luftfeuchtigkeit folglich nicht zugerechnet; siehe auch Wikipedia – Luftfeuchtigkeit. Der Ausdruck Feuchtigkeit (Moisture) oder Feuchte kennzeichnet das Maß der Anwesenheit von Wasser in oder an einem Material (z. B. Textilien) oder einer Substanz oder in einem Gas oder in einem Raum. Im Weiteren wird die Luft als binäres Stoffgemisch aus trockener Luft und Wasserdampf betrachtet.
Feuchtemodelle
Die Konvektions-Diffusions-Gleichung, die den Feuchtetransport im Gewächshaus beschreibt, basiert auf dem ersten Fickschen Gesetz und lautet:
\[
\frac{\partial \phi}{\partial t} + \mathbf{u} \cdot \nabla \phi = \nabla \cdot (D \nabla \phi)
\]
Hierbei steht \( \phi \) für die Stoffmengenkonzentration, \( t \) für die Zeit, \( \mathbf{u} \) für den Geschwindigkeitsvektor aus der Strömung und \( D \) für den Diffusionskoeffizienten.
etwas mehr zur Konvektions-Diffusions-Gleichung (klicke hier)
Die Gleichung beschreibt, wie sich die (Feuchte-) Konzentration \( \phi \) im Laufe der Zeit ändert. Der erste Term auf der linken Seite (\( \frac{\partial \phi}{\partial t} \)) repräsentiert die zeitliche Änderung der Konzentration. Der zweite Term (\( \mathbf{u} \cdot \nabla \phi \)) beschreibt den Beitrag der Konvektion zur Änderung der Konzentration, wobei \( \mathbf{u} \) die Geschwindigkeit des Fluids und \( \nabla \phi \) den Konzentrationsgradienten darstellt. Der dritte Term (\( \nabla \cdot (D \nabla \phi) \)) repräsentiert den Beitrag der Diffusion zur Änderung der Konzentration.
Für die numerische Simulation integrieren wir diese Gleichung in einen OpenFOAM-Solver.
Kopplung zur Strömung
Die Transportgleichung hängt vom Geschwindigkeitsfeld \( \mathbf{u} \) ab, während die Feuchteverteilung bisher keine Auswirkung auf die Strömung hat. Um eine Kopplung zwischen dem Feuchtigkeitsmodell und der Impulsgleichung der Strömung herzustellen, verwenden wir eine modifizierte Boussinesq-Approximation für die Dichte (Sosnowski[1][2], Limane[3]). Sie berücksichtigt die Ausdehnung von Fluiden aufgrund von Temperatur- und Feuchtigkeitsänderungen und wird wie folgt berechnet:
\[
\rho = \rho_0 \left(1 – \beta_T (T – T_\infty) – \beta_\omega (\omega – \omega_\infty)\right)
\]
etwas mehr zur Boussinesq-Approximation (klicke hier)
Dabei sind \( \rho_0 \) die Referenzdichte, \( \beta_T \) der Volumenexpansionskoeffizient in Bezug auf die Temperatur, \( T \) die Temperatur, \( T_\infty \) die Referenztemperatur, \( \beta_\omega \) der Volumenexpansionskoeffizient in Bezug auf die Feuchtigkeit, \( \omega \) die Feuchtigkeitskonzentration und \( \omega_\infty \) die Referenzfeuchtigkeit.
Diese modifizierte Dichteanpassung ermöglicht es, dass Strömungen nicht nur durch Temperatur-unterschiede, sondern auch durch Unterschiede in der Wasserdampfkonzentration induziert werden. Dadurch können Phänomene wie natürliche Konvektion aufgrund von Feuchtigkeitsunterschieden modelliert werden.
OpenFOAM-Solver
Angetrieben durch die Solareinstrahlung (natürliche/freie Konvektion) oder eine Entlüftung über Ventilatoren entwickelt sich im Gewächshaus eine Strömung. Angesichts niedriger Strömungsgeschwindigkeiten gehen wir davon aus, dass wir das Verhalten der Luft gut durch einen inkompressiblen Ansatz beschreiben können. Das Programmpaket OpenFOAM (Open Source Field Operation and Manipulation) stellt für diese Situation, d. h. Berücksichtigung der Temperatur und der Auftriebseffekte (buoyant), mehrere Solver zur Verfügung:
- buoyantBoussinesqPimpleFoam
- buoyantPimpleFoam
- chtMultiRegionFoam
- sowie jeweils stationäre Varianten dieser Verfahren
OpenFOAM ist kein monolithischer Strömungslöser, sondern besteht aus einer Vielzahl von C++-Klassen und dazugehörigen Librarys, die es ermöglichen für eine bestimmte Situation einen geeigneten Strömungslöser zu bauen. Weiterhin erlaubt die Modifikation des Quelltextes eines vorhandenen Lösers, die Aufnahme von weiteren Gleichungen, wie etwa das Feuchtemodell oder die Transportgleichung, Randbedingungen und zusätzlichen Ausgaben. Technische Voraussetzung hierfür ist eine funktionierende OpenFOAM-Umgebung, die die Neukompilierung mit dem Tool wmake gestattet. Mehr Informationen dazu finden sich auf der OpenFOAM-webpage, insbesondere unter OpenFOAM® System Requirements und im Programmer’s Guide.
Wir haben die folgenden Solver für die unterschiedlichen Fragestellungen entwickelt:
- gwr-AoA: age of air
- gwr-humidity-passiv: In diesem Ansatz wird die Konvektions-Diffusions-Gleichung in das Modell aufgenommen, aber die Kopplung über die modifizierte Boussinesq-Approximation entfält. Die relative Luftfeuchte ist hier ein passives Skalar.
- gwr-humidity: gekoppeltes Feuchtemodell
Solarmodell
Beschreibung zum Solarmodell (klicke hier)
Von der Erde aus erscheint die Sonne als isotherme Kreisscheibe \(A_{sun}\), die einem schwarzen Körper mit der Temperatur \(T_{sun} = 5780\) K entspricht. Sind \(\alpha_s\) der Sonnenazimut- und \(\gamma_s\) der Sonnenhöhenwinkel, so ist die Position der Sonne gegeben durch
\[
{\bf s} = r_{sun} \begin{bmatrix}
\cos \alpha_s \; \cos \gamma_s \\
-\sin \alpha_s \, \cos \gamma_s \\
\sin \gamma_s
\end{bmatrix} , \qquad r_{sun} = 1.5 \cdot 10^8 \text{ km }.
\] Die Simulation verwendet den Ort (Längen- und Breitengrad), das Datum und die Tageszeit gemäß DIN 5034-2, um die Position der Sonne zu bestimmen. Darüber hinaus ermöglicht das Modell eine Ausrichtung relativ zur Nordrichtung. Eine grafische Benutzeroberfläche (GUI) generiert entsprechende Daten für die Startposition in den Steuerdateien.
Die Aufnahme der Sonne \(A_{sun}\) in die Menge der Oberflächen (Umhüllungen) führt letztlich zu einem weiteren Quellterm in der Gleichung für die Helligkeiten im Gewächshaus.
\[
q_{\rm out} ({\bf x}) = \epsilon \,\sigma \, T^4({\bf x}) + \rho \, q_{sun}({\bf x}) + \rho \, ( {\mathcal K} q_{\rm out} )({\bf x}),
\] wobei \[
q_{sun}({\bf x}) = vis({\bf x},A_{sun}) \, E_0 \, \cos \phi_{\bf x} \quad [ {\rm W/m^2} ]
\] Dabei entscheidet die Auswertung der Funktion \(vis({\bf x},A_{sun})\), ob der Oberflächenpunkt \({\bf x}\) die Sonne sieht (direkte Bestrahlung) oder nicht (Lage im Schatten).
Während des Simulationsverlaufs ändert sich die Position der Sonne je nach Zeitpunkt, was sich auf ihre Sichtbarkeit und somit auch auf den Quellterm der Energiegleichung auswirkt. In Abb. 1 ist die direkte Solareinstrahlung für ein vereinfachtes Modell dargestellt. Ohne Einfluss der Atmosphäre ist die Bestrahlungsstärke \(E_0=1361\) \([{\rm W/m^2} ]\) (Solarkonstante), für einen konkreten Anwendungsfall sind entweder Messwerte, d.h. ein Tagesgang in Form einer Datei mit entsprechenden Daten, oder ein analytisches Modell für die Bestrahlungsstärke vorzugeben.
Vereinfachtes Transparenzmodell
Die Baugruppen, die als durchsichtig für die Sonne gekennzeichnet sind (wie das Kuppeldach und die Fenster), lassen externe Strahlung in den Innenraum eindringen. Dabei werden die Materialien dieser Baugruppen, wie Folie und Glas, mit einem Transmissionskoeffizienten und einem Brechungsindex versehen. Eine transparente Schicht erwärmt sich durch Absorption der direkten Solarstrahlung \( \alpha \, q_{sun}\), der Teil \(\tau \, q_{sun}\) gelangt in den Innenraum (gerichtet und diffus), jedoch nicht wieder hinaus. Diese selektive Transparenz ermöglicht eine Berücksichtigung des Treibhauseffekts.
Gewächshaussimulation
Abb. 2 zeigt den Temperaturverlauf zu einer Simulation für das vereinfachte Gewächshaus mit dem Solarmodell (Wärmeleitung, Strahlung, keine Lüftung) in 3 Monitorpunkten. Eine Positionierung der (virtuellen) Messpunkte kann wieder übers GUI erfolgen, wobei die Anzahl der Monitorpunkte und auch deren Lage ist frei wählbar. Hier liegen sie an den Wänden und am Boden.
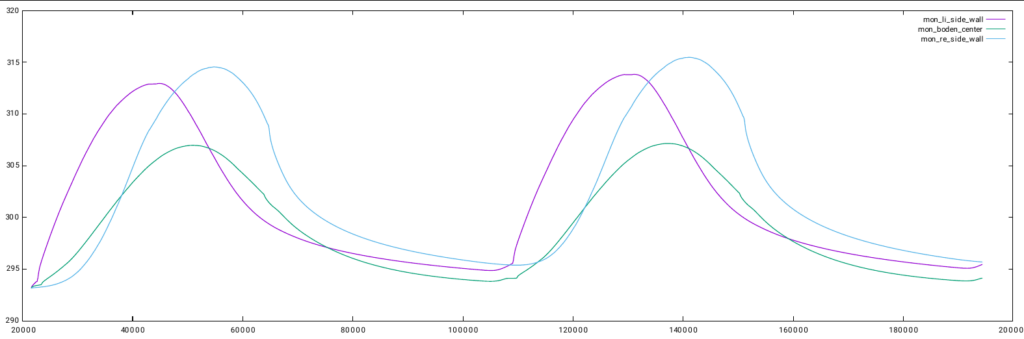
Das Modell besteht aus ca. 77500 Oberflächen- und ca. 1.7 Mio. Solidelementen. Die Rechnung wurde auf einer Workstation der GWR GmbH durchgeführt und benötigte für den Simulationszeitraum von 48 h eine Rechenzeit von 14 h bei einer Zeitschrittweite von \(\delta t=10 \, s\) (Stand 2021).
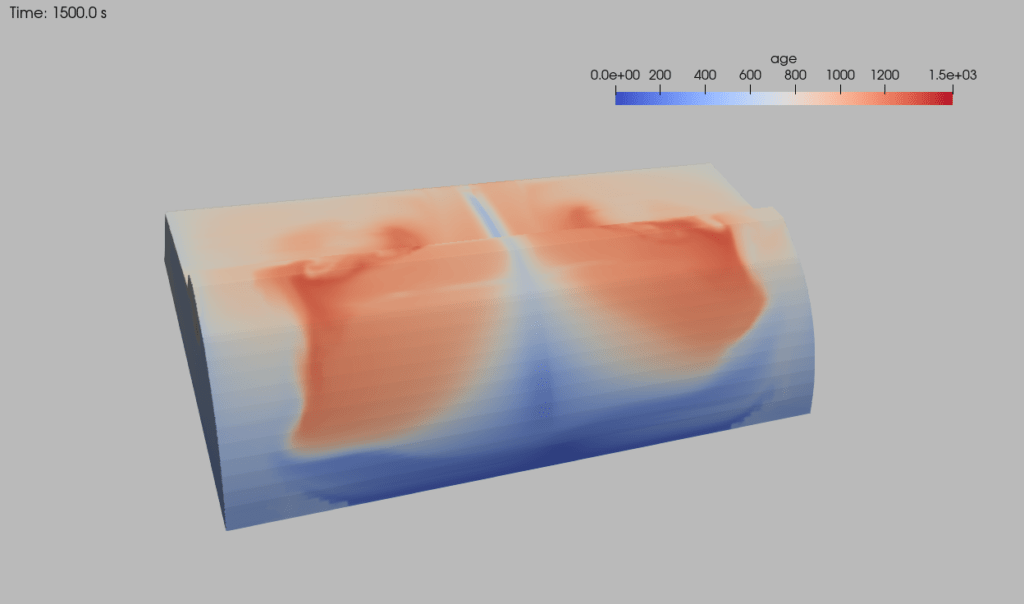
Age of air (AoA) — Mathematisches Modell zur Berechnung der Frischluftverteilung
Die Age of Air Theorie (kurz AoA) ist ein mathematischer Ansatz zur Bestimmung der Verweildauer von Luftpartikeln in einem Raum. Dieser Ansatz wird verwendet, um die Effizienz von Lüftungssystemen zu bewerten und Aussagen über die Verteilung und den Anteil der Frischluft in geschlossenen Räumen zu treffen. Indem das mittlere Alter der Luft berechnet wird, lässt sich nachvollziehen, wie gut und wie schnell verbrauchte Luft gegen frische Luft ausgetauscht wird.
Ausgangspunkt für die Berechnung des mittleren Luftalters ist die folgende Transportgleichung,
siehe auch Bartak[4], Davisson[5] oder Sandberg[6].
\begin{equation} \label{eq:AoA}
\frac{\partial \tau}{dt} + \mathbf{\nabla} \cdot ( \bf{u} \, \tau – D\, \nabla \tau ) = 1
\end{equation}
mit den Randbedingungen
\[
\begin{aligned}
\tau &= 0 \quad \text{ für das Inlet (Frischluft)} \\
\frac{\partial \tau}{d n } &= 0 \quad \text{ an allen Wänden und am Outlet. }
\end{aligned}
\]
und der Anfangsbedingung \(\tau({\bf x},0) = \tau_0 \), wobei \(\tau_0\) das Alter der Luft zum Zeitpunkt \(t=0\) ist. Die Variable \(\bf{u}\) repräsentiert hierbei das Geschwindigkeitsfeld der Strömung und gibt an, wie sich die Luft in dem Raum bewegt.
Die rechte Seite der Differentialgleichung besagt, dass das Alter der Luft pro Zeiteinheit konstant zunimmt. Streichen wir den Diffusions- und Transportterm und setzen die Anfangsbedingung auf \( \tau_0 \), so bleibt eine vereinfachte Form, die nur die zeitliche Zunahme des Luftalters beschreibt. Die Gleichung reduziert sich dann auf:
\[\frac{\partial \tau}{\partial t} = 1\]
Mit der Anfangsbedingung \( \tau(0) = \tau_0 \) führt dies zur Lösung:
\[\tau(t) = t + \tau_0\]
Die Lösung zeigt, dass das Luftalter linear mit der Zeit wächst, beginnend bei \( \tau_0 \). Dies beschreibt eine Umgebung ohne Frischluftzufuhr, in der die Luft gleichmäßig altert.
Die Lösung von \eqref{eq:AoA} ist dann das mittlere Alter $\tau$ der Luft im Berechnungsgebiet. Für die Simulation wird der OpenFOAM Solver pimplefoam um die Gleichung \eqref{eq:AoA} ergänzt. Da \(\tau\) keine Wirkung auf das Strömungsfeld hat, ist es wieder ein passives Skalar.
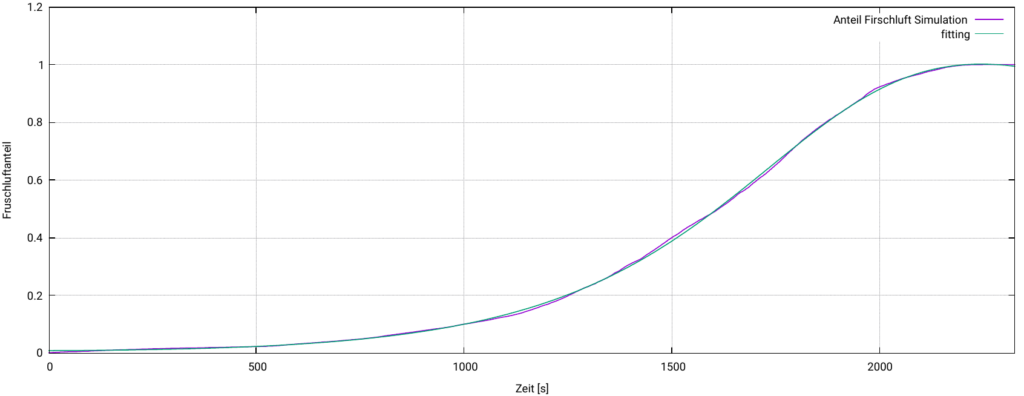
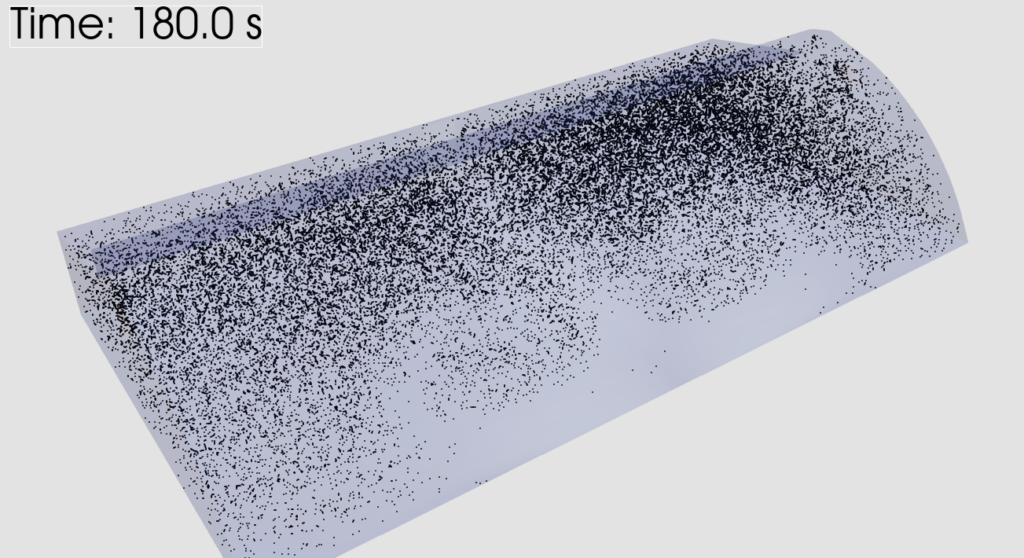
Quellen
- (2013): Numerical model for thin liquid film with evaporation and condensation on solid surfaces in systems with conjugated heat transfer. In: International Journal of Heat and Mass Transfer, Bd. 66, S. 382–395, 2013, ISSN: 0017-9310.
- (2013): Numerical investigation of evaporation and condensation of thin films in conjugated heat transfer systems. 2013.
- (2017): Simulation of airflow with heat and mass transfer in an indoor swimming pool by OpenFOAM. In: International Journal of Heat and Mass Transfer, Bd. 109, S. 862-878, 2017.
- (2001): Experimental and numerical study of local mean age of air. In: (IBPSA), International Building Performance Simulation Association (Hrsg.): 2001.
- (1987): Calculation of age and local purging flow rate in rooms. In: Building and Environment, Bd. 22, Nr. 2, S. 111–127, 1987, ISSN: 0360-1323.
- (1981): What is ventilation efficiency?. In: Building and Environment, Bd. 16, Nr. 2, S. 123–135, 1981, ISSN: 0360-1323.