\(
\def\x{{\bf x}}
\def\y{{\bf y}}
\def\out{{\rm out}}
\newcommand{\Spro}[2]{\langle {#1},{#2} \rangle}
\)
Die radiosity equation ist eine Integralgleichung, die den Strahlungs- bzw. Energieaustausch zwischen diffusen grauen Oberflächen modelliert. Sie lautet
\begin{equation} \label{IGLqout2}
q_\out (\x) = \epsilon \, \sigma \, T^4(\x) + \rho \, \int_\Gamma k(\x,\y) \, q_\out (\y) \, d\y,
\end{equation}
für einen Punkte $\x$ auf der Oberfläche $\Gamma$. Die radiosity equation ist eine vereinfachte Version der rendering equation für diffuse Oberflächen.
Die Gleichung \eqref{IGLqout2} repräsentiert keinen Zusammenhang zwischen diskreten Größen, sondern wird im Rahmen eines Funktionenraums betrachtet. Das bedeutet, dass $q_\out$, $T$ und der Kern $k$ Funktionen sind, die bestimmte (Regularitäts-) Eigenschaften haben. Dies führt zur Fredholm-Theorie, in der die Gleichung üblicherweise mit einem Integraloperator $\mathcal{K}$ dargestellt wird:
$$
( I – {\mathcal K} ) \, q_{\rm out} (\x) = \epsilon \, \sigma \, T^4(\x) , \quad \forall \x \in \Gamma .
$$
Ausgehend von den Temperaturen auf den beteiligten Oberflächen wird die entsprechende Helligkeit, d.h. die Ausstrahlung oder radiance, durch $\eqref{IGLqout2}$ festgelegt. Eine besondere Rolle spielt hierbei die Sichtbarkeitsfunktion. Obwohl sie auf den ersten Blick harmlos erscheint, entwickelt sich ihre Berechnung zu einem ernsthaften Problem hinsichtlich des erforderlichen Rechenaufwands, siehe Visibility.
Bezeichnungen
Bezeichnungen (klicke hier)
- $\Gamma$ eine Oberfläche in $\mathbb{R}^3$
- $T(\x)$ die Temperatur im Oberflächenpunkt $\x$,
- $q_{\rm out}$ die Helligkeit eines Paneels
- $\epsilon$ der Emissionsgrad, $\rho=1-\epsilon$ der Reflexionsgrad und $\sigma$ die Stefan-Boltzmann Konstante,
- $ $
\begin{equation} \label{kern3D}
k(\x,\y) := \frac{\cos \phi_\x \, \cos \phi_\y }{\pi \; \|\x-\y\|^2} \, \chi(\x,\y), \qquad \x,\y \in \Gamma,
\end{equation}
der Kern des Integraloperators $\mathcal{K}$
\begin{equation} \label{Kdef}
({\mathcal K} \, q )(\x) := \rho \, \int_\Gamma k(\x,\y) \, q (\y) \; d\y, \quad \x \in \Gamma,
\end{equation}
- $ \chi(\x,\y)$ die visibility-Funktion, siehe hier.
Numerische Lösung
Für die numerische Lösung auf einem Computer muss die kontinuierliche Gleichung \eqref{IGLqout2} in ein diskretes System überführt werden. Dies kann durch verschiedene Methoden erfolgen, darunter das Kollokations- und das Galerkin-Verfahren. Die Diskretisierung der radiosity equation mit dem Kollokationsverfahren führt auf ein lineares Gleichungssystem der Form
\begin{equation} \label{DCR}
(I_n – K_n) \, q_n = E_n
\end{equation}
mit
- $n$ der Anzahl der Panelle (geometrische Diskretisierung der Oberfläche),
- der vollbesetzten(!) Matrix $K_n \in \mathbb{R}^{n \times n}$, die Viewfactor-Matrix (Cohen[1]),
- dem $n$-dimensionalen Vektor $q_n \in \mathbb{R}^n$, die gesuchten Wärmestromdichten (Helligkeit) bzgl. der Paneele
- und der bekannten rechte Seite (die Quellen) $E_n \in \mathbb{R}^n$ .
Für feine Diskretisierungen, d.h. großes $n$, ist die Rechenzeit zur Bestimmung und der Aufwand zur Speicherung für die $n^2$ Koeffizienten der Matrix $K_n$ nicht mehr akzeptabel. So sind bei einfacher Floating-Point-Genauigkeit \(4 \, n^2\) Byte zur Speicherung erforderlich. Die folgende Tabelle enthält einige Werte zum Speicherplatzbedarf der Viewfactor-Matrix:
| $n$ | 1000 | 100000 | 250000 | 1000000 | 5000000 |
|---|---|---|---|---|---|
| $4\, n^2$ byte | 3.81 [MB] | 38.1 [GB] | 238.4 [GB] | 3.8 [TB] | 95.3 [TB] |
Ist ein Modell mit 5 Millionen Oberflächenelementen aufgelöst, so benötigt die Berechnung der vollen Viewfactor-Matrix eine Speicherplatzbelegung von 95,3 TB. Wenn man davon ausgeht, dass die Systemmatrix auf einem Cluster verteilt ist, entspricht dies etwa 186 Workstations mit jeweils 512 GB RAM-Speicher.
Iteratives Verfahren
Ein iteratives Lösungsverfahren für das Gleichungssystem (4) erfordert nicht zwingend die explizite Kenntnis der Matrix $K_n$. Stattdessen genügt es, wenn ein Algorithmus für die Matrix-Vektor-Multiplikation
\begin{equation} \label{MatVek}
(K_n \, q_n)_i = \sum_{j=1}^n q_j \int_{t_j} k(\xi_i, \y) \, d\y, \quad i=1,\ldots,n ,
\end{equation}
vorhanden ist. Die Idee besteht nun darin, nicht mehr die Matrix $K_n$ zu berechnen, sondern eine sinnvolle Approximation der Matrix-Vektor-Multiplikation $K_n q_n$ zu finden. Dies wird durch eine spezielle Nahfeld-Fernfeld-Zerlegung, das sogenannte panel clustering, ermöglicht.
panel clustering
Die Entwicklung eines funktionierenden Verfahrens zur numerischen Lösung der Gleichung \eqref{IGLqout2} mittels panel clustering[2] ist anspruchsvoll und erfordert einen hohen Arbeitsaufwand. Insbesondere sind die folgenden Punkte zu beachten:
- Als notwendige Voraussetzung zum Panel-Clustering ist aus der geometrischen Diskretisierung ein sogenannter Clusterbaum zu bestimmen.
- Es bedarf einer Datenstruktur für den “Panel-Clustering Operator”, um die (approximierte) Matrix-Vektor-Multiplikation effizient zu berechnen.
- Das Auftreten von schwach singulären Integralen im Nahfeld muss berücksichtigt werden.
- Es ist erforderlich, die Sichtbarkeiten zu bestimmen und entsprechende Datenstrukturen zu implementieren,
- und schließlich braucht man noch ein passendes iteratives Verfahren, um die diskrete Gleichung \eqref{DCR} zu lösen.
Das Panel-Clustering-Verfahren bietet deutliche Vorteile gegenüber klassischen Methoden, insbesondere im Vergleich zur Verwendung der vollen Viewfactor-Matrix:
- Durch das Panel-Clustering wird der Speicherplatzbedarf erheblich reduziert, was die Durchführung der numerischen Lösung auf einer Workstation oder wenigen Clusterknoten erst ermöglicht.
- Schnelle Matrix-Vektor-Multiplikation und damit auch eine schnellere Lösung des diskreten GLeichungssystems.
Bei der Wahl des iterativen Lösers kann man eine positive Eigenschaft der radiosity equation nutzen, deren Darstellung hier den Rahmen sprengen würde. Eine Variante des BiCG-Verfahrens[3] hat sich als äußerst erfolgreich erwiesen. Dabei zeigt sich ein sehr interessantes Phänomen: Die Konvergenzrate verschlechtert sich nicht mit einer geometrischen Verfeinerung, also mit einer höheren Dimension der Diskretisierungsmatrix. Sie ist unabhängig von der Dimension des Gleichungssystems.
Beispiel
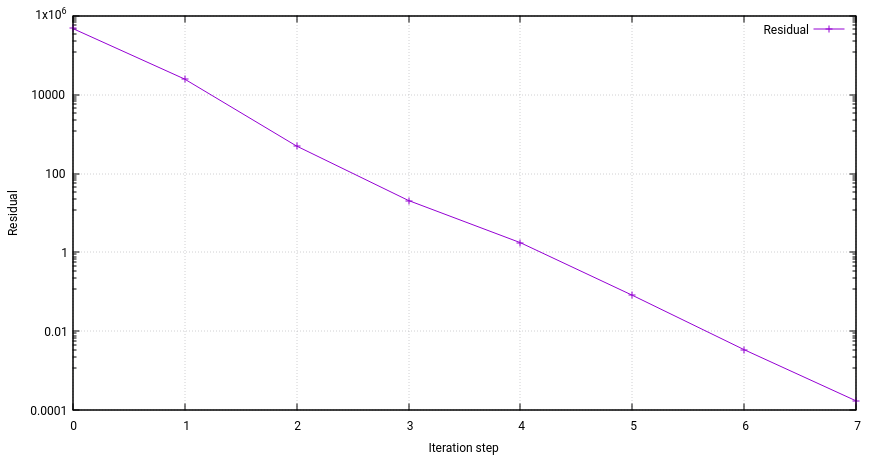
Der nachfolgende Plot zeigt den Verlauf der Iterationen für ein Testproblem mit 155640 Freiheitsgraden. Bereits nach 7 Iterationen wurde eine hinreichend genaue Lösung ermittelt, für die die eingesetzte Workstation (Ryzen 9 5950X-Prozessor mit 16 Kernen) lediglich 1.4 Sekunden benötigte.
Im Vergleich zum klassischen Verfahren, das etwa 90 GB Speicher für die Berechnung der vollen Viewfactor-Matrix erfordern würde, kam das gesamte Programm nur etwa 4,5 GB (einschließlich der Wärmeleitungsberechnung) aus. Davon entfielen nur ca. 1 GB auf das Panel-Clustering-Verfahren.
Bestrahlungsstärke (Irradiance)
Die im Punkt $\x$ eingestrahlte Energiestromdichte $q_{\rm in}$ ist die Summe aller $q_{\rm out} (\y)$, die auf $\x$ “fallen”. Mit einer geometrischen Betrachtung über den Raumwinkel findet sich ein analytischer Ausdruck mit dem die eingestrahlte Energie (-stromdichte) in Abhängigkeit von $q_{\rm out}$ angegeben werden kann (Siegel[4]):
\begin{equation} \label{IGL1}
q_{\rm in} (\x) = \int_\Gamma k(\x,\y) \, q_{\rm out}(\y) \; d\y = \mathcal{K} q_{\rm out}(\x), \quad \forall \x \in \Gamma .
\end{equation}
Die Einstrahlung in einem Punkt $\x$ der Oberfläche ergibt sich durch Anwendung des Integraloperators $\mathcal{K}$ auf die Lösung der Gleichung $\eqref{IGLqout2}$.
Zur (Netto-) Wärmebilanz (klicke hier)
Bemerkung 1
Für die (Netto-) Wärmebilanz
$$
q(\x) = q_{\rm out}(\x) – q_{\rm in}(\x), \quad \x \in \Gamma
$$
gelten die Gleichungen
\begin{align}
q(\x) & = \epsilon \, \sigma \, T^4(\x) – \epsilon \, q_{\rm in} (\x), \nonumber \\
q(\x) & = \frac{ \epsilon}{1-\epsilon} \left( \sigma T^4(\x) – q_{\rm out}(\x)\right), \quad \epsilon \not=1, \nonumber
\end{align}
und
\begin{equation}
q(\x) = q_{\rm out}(\x) – \int_A k(\x,\y) q_{\rm out}(\y) \; d\y \nonumber
= \left( ({\mathcal I} -{\mathcal K})q_{\rm out} \right) (\x). \label{Q2}
\end{equation}
Bei bekannter Energiestromdichte $q$ berechnet sich der (Netto-) Wärmestrom auf einer (Teil-) Oberfläche $S \subset \Gamma$ zu
$$
\dot{Q} = \Phi = \int_S q(s) \, ds .
$$
Bemerkung 2
Für eine schwarze Oberfläche gilt:
- Die Ausstrahlung ist gleich der Emission, da keine einfallende Strahlung reflektiert wird
\begin{equation} \label{qoutblackbody}
q_{out} = \sigma \, T^4 \quad \left[\frac{W}{m^2}\right].
\end{equation} - Die einfallende Strahlung wird vollständig absorbiert, d.h. die Nettowärmestromdichte ist
$$
q_{netto} = \sigma \, T^4 – q_{in} .
$$
Sind alle beteiligten Oberflächen schwarze Strahler, dann gilt
$$
q_{netto}(\x) = \sigma \, T^4(\x) – \int_\Gamma k(\x,\y) \sigma \, T^4(\y) d\y
$$
(die Gleichung folgt aus $\eqref{IGL1}$ und $\eqref{qoutblackbody}$) .
Quellen
- (1993): Radiosity and Realistic Image Synthesis. 1993, ISBN: 0121782700.
- (1989): On the fast matrix multiplication in the boundary element method by panel clustering. In: Numerische Mathematik, Bd. 54, Nr. 4, S. 463–491, 1989, ISSN: 0945-3245.
- (1992): BiCGSTAB: A fast and smoothly converging variant of Bi–CG for the solution of nonsymmetric linear systems.. In: SIAM J. Sci. Statist. Comput., Bd. 13, Nr. 2, S. 631–644, 1992.
- (2002): Thermal Radiation Heat Transfer. 4th Edition, Taylor & Francis, New York, London, 2002.