Der Temperaturverlauf in der Umgebung eines Kontaktbereiches wird mithilfe des nachfolgenden Modellproblems analysiert (1D-Interface Problem). Für die numerische Lösung der heat equation in komplizierten 3-D-Geometrien lassen sich hiermit Rückschlüsse zur Auflösung des evtl. großen Temperaturgradienten (Feinheit des Gitters im Kontaktbereich) bzw. zur Konstruktion von Ansatzfunktionen fürs XFEM-Verfahren gewinnen.
Das Modellproblem
Zwei, jeweils einseitig unendlich ausgedehnte Körper mit verschiedenen Anfangstemperaturen, berühren sich bei \(x=0\). In beiden Gebieten gilt die Wärmeleitungsgleichung:
$$
\frac{\partial}{\partial t} T_1(x,t) = a_1 \, \frac{\partial T_1 (x,t)}{\partial^2 x}, \qquad \text{mit}
\qquad T_1(x,0) = T_{1}, \quad T_1(-\infty,t) = T_1, \quad x < 0, \quad t > 0,
$$
und
$$
\frac{\partial}{\partial t} T_2(x,t) = a_2\, \frac{\partial T_2(x,t)}{\partial^2 x} \qquad \text{mit}
\qquad T_2(x,0) = T_{2}, \qquad T_2(\infty,t) = T_2, \quad x >0, \quad t >0.
$$
mit den Temperaturleitfähigkeiten
$$
a_i = \frac{\lambda_i}{\rho_i \, c_i} \quad \left[ \frac{m^2}{s} \right] , \quad i=1,2 .
$$
Die Kontaktbedingungen für \(x=0\) sind
$$
T_1(0,t) = T_2(0,t) \quad \text{ und } \quad \lambda_1 \, \frac{\partial T_1}{\partial n} (0,t)= \lambda_2 \, \frac{\partial T_2}{\partial n}(0,t) .
$$
Einsetzen der Ansatzfunktionen, die beide die Wärmeleitungsgleichung erfüllen,
$$
T_1(x,t) = A_1 + \, B_1 \, {\rm erf} \left( \frac{-x}{\sqrt{4\, a_1 \,t}}\right) , \quad x < 0 $$ und $$ T_2(x,t) = A_2 + \, B_2 \, {\rm erf} \left( \frac{x}{\sqrt{4\, a_2 \,t}}\right) , \quad x > 0.
$$
in die Kontaktbedingungen ergibt die Lösung
$$
T_1(x,t) = T_C \, + \, \frac{ \beta_{2}}{\beta_{1} + \beta_{2}} \, {\left(T_{1} – T_{2}\right)} \, {\rm erf} \left( \frac{-x}{\sqrt{4\, a_1 \,t}}\right) , \quad x < 0, \; t>0
$$
auf der negativen Halbachse und für \(x>0\)
$$
T_2(x,t) = T_C \, – \, \frac{ \beta_{1}}{\beta_{1} + \beta_{2}} \, {\left(T_{1} – T_{2}\right)} \, {\rm erf} \left( \frac{x}{\sqrt{4\, a_2 \,t}}\right) , \quad x > 0, \; t>0 .
$$
Die zeitunabhängige Kontakttemperatur ist \(T_C\):
\begin{equation} \label{Tc}
T_C= \frac{T_{1} \beta_{1} + T_{2} \beta_{2}}{\beta_{1} + \beta_{2}} =
T_{1} + \frac{\beta_{2}}{ \beta_{1} + \beta_{2} } \left( T_{2} – T_{1}\right) .
\end{equation}
Die Materialkonstanten
$$
\beta_i:= \sqrt{\lambda_i \, \rho_i \, c_i} \quad \left[ \frac{J}{K \, m^2 s^{1/2}} \right] , \quad i=1,2
$$
werden als Wärmeeindringkoeffizienten bezeichnet.
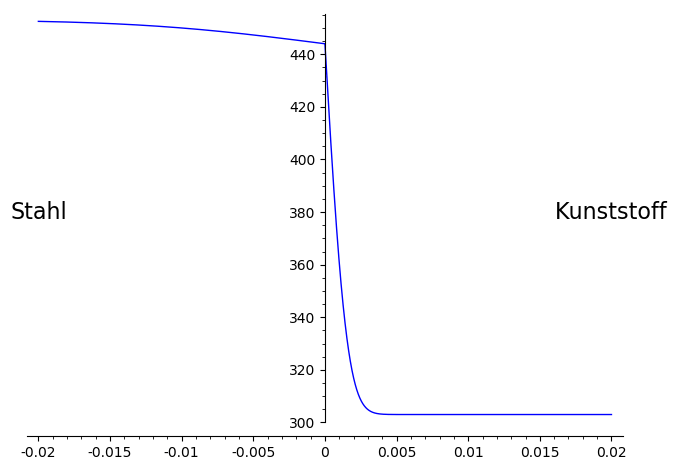
Kontakt zwischen Stahl und Kunststoff
Als Beispiel zum 1D-Interface-Problem betrachten wir die Materialien Stahl (linker Körper)
$$\lambda_1 = 40 \left[ \frac{W}{m\, K} \right], \quad \rho_1= 7850 \left[ \frac{kg}{m^3} \right] \quad c_1 = 480 \left[ \frac{J}{kg\, K} \right],$$
$$\qquad a = 1.0615 \times 10^{-5} \quad \left[ \frac{m^2}{s} \right]$$
und Kunststoff (rechts)
$$\lambda_2 = 0.3 \left[ \frac{W}{m\, K} \right], \quad \rho_2= 1700 \left[ \frac{kg}{m^3} \right] \quad c_2 = 1200 \left[ \frac{J}{kg\, K} \right],$$
$$\qquad a = 1.4706 \times 10^{-7} \quad \left[ \frac{m^2}{s} \right]$$
Die Wärmeeindringkoeffizienten sind
$$
\beta_1 = 12276.80 \qquad \text{ und } \quad \beta_2= 782.30 \qquad \left[ \frac{J}{K \, m^2 s^{1/2}} \right]
$$
Mit den Anfangstemperaturen von \(T_{1}=453 \, [K]\) für den Stahl und \(T_{2}=303 \, [K]\) für den Kunststoff ist die Kontakttemperatur nach \eqref{Tc}
$$
T(0,t) = 444.014 \quad \left[ K \right].
$$
SageMath-Script
Der Temperaturverlauf für \(t=5 \, s\) ist in der obigen Abbildung dargestellt und kann mithilfe eines SageMath-Scripts berechnet werden (mehr Informationen zu SageMath und seiner Nutzung findet sich hier)