SageMath

SageMathCell

SageMath ist ein quelloffenes und kostenloses Computeralgebrasystem (CAS). Es erlaubt das Umstellen, Faktorisieren, Vereinfachen, Differenzieren und Integrieren von Termen (symbolischen Ausdrücken) – und bietet darüber hinaus viele weitere Möglichkeiten. Mit SageMathCell lassen sich solche Berechnungen sogar direkt online in einer Web-Oberfläche durchführen, wobei eine Python-ähnliche Skriptsprache zum Einsatz kommt.

Beispiele

oder auch mit LaTeX-Ausgabe

und auch als plot

Eine Eingabe von Parametern ist ebenfalls möglich

Collatz-Problem

Die Collatz-Funktion nimmt eine positive ganze Zahl als Eingabe und berechnet daraus eine neue ganze Zahl nach folgender Vorschrift: \[ f(n) = \begin{cases} \frac{n}{2} & \text{falls } n \text{ gerade ist} \\ 3n + 1 & \text{falls } n \text{ ungerade ist} \end{cases}, \qquad n \in \mathbb{N}. \] Der Collatz-Orbit ist eine Folge von Zahlen, deren erster Eintrag durch die Anwendung dieser Funktion auf eine bestimmte Ausgangszahl entsteht, und deren weitere Elemente aus dem aktuellen Vorgänger berechnet werden, bis der Wert 1 erreicht wird:

\[ O_0=n, \quad O_{i+1} = f(O_i), \qquad \text{Stopp, falls } O_i = 1. \] Die Collatz-Vermutung besagt, dass für alle natürlichen Zahlen die Folge irgendwann stoppt. Sie ist eine berühmte ungelöste mathematische Fragestellung.

• Wikipedia Collatz-Problem
• Jeffrey C. Lagarias: The 3x+1 Problem: An Overview
• G.J. Wirsching: Das Collatz-Problem

Berechnung der hemisphärischen Kugelflächenfunktionen

An dieser Stelle verwenden wir SageMath zur Visualisierung der Pyramide der Basisfunktionen zu den hemisphärischen Kugelflächenfunktionen. Das entsprechende SageMath-Script ist etwas umfangreicher und sieht wie folgt aus:

# Normierungsfaktoren 
def Klm(l,m):
    if (m<0):
        return Klm(l,-m)
    return sqrt( (2*l+1)/(2*pi) * factorial(l-m)/factorial(l+m))
#
# assoziierte Legendrepolynomen
def P_shift(l,m,x):
    return gen_legendre_P( l,m,(2*x-1))
#
# Die Basisfunktionen 
#
def hsh(l,m,x,y):
    if m == 0:
        return Klm(l,0)*P_shift(l,m,cos(x))
    if m < 0: 
        return sqrt(2)*Klm(l,-m)*P_shift(l,-m,cos(x))*sin(-m*y) 
    if m > 0:
        return sqrt(2)*Klm(l,m)*P_shift(l,m,cos(x))*cos(m*y)
#
var("theta,phi,l,m")
#
#
# Anmerkung: 
#  * srange statt range, sonst hat gen_legendre_P ein Problem
#  * siehe https://ask.sagemath.org/question/8131/attributeerror-int-object-has-no-attribute-mod/
# statt über die for-loops 
# for l in srange(0,5):
#    for m in srange(-l,l+1): 
# zur Erzeugung aller Basisfunktionen, hier jetzt ein "interact" zur 
# Auswahl der Parameter von l und m, für m muss -l <= m <= l gelten.
# 
@interact
def data(l=(4,srange(4,5)), m=(2,srange(-4,5))):
        Y=hsh(l,m,theta,phi)
        rea = spherical_plot3d( max_symbolic(Y,0.0), (phi,0,2*pi), (theta,0.0,pi/2), 
                                color='blue', plot_points=(80,80), opacity=0.9)
        ima = spherical_plot3d( abs(min_symbolic(Y,0.0)), (phi,0,2*pi), (theta,0.0,pi/2), 
                                color='green', plot_points=(80,80), opacity=0.9)
        (rea+ima).show(aspect_ratio=1)

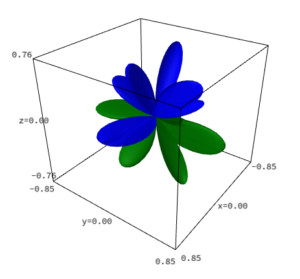
• die Parameter l und m können direkt im Script geändert werden (Zeile 22). Aber Achtung: für m muss -l < m <= l gelten.

SageMath-Code aus externer Datei einbinden

Wenn SageMath-Code umfangreich oder mehrfach verwendet wird, ist es sinnvoll, ihn nicht direkt im HTML einzubetten, sondern als externe Datei auszulagern. Dies verbessert die Wartbarkeit, vermeidet Formatierungsfehler (z. B. durch Tabs und Leerzeichen) und macht die Struktur der Webseite übersichtlicher.

Vorteile der Auslagerung

• Zentrale Pflege: Änderungen am Code sind nur in der Datei nötig.
• Wiederverwendbarkeit: Die gleiche Datei kann in mehreren Beiträgen verwendet werden.
• Saubere WordPress-Integration: Tabs, Leerzeichen und Formatierungsprobleme entfallen. Kein visueller Editor oder Block-Umbruch zerstört die Syntax.

Schritt-für-Schritt: Sage-Datei einbinden

Datei erstellen

Speichere den Sage-Code als Datei, z. B.:

ParameterIdentifikation.sage

Datei hochladen

Lade die Datei per FTP (z. B. FileZilla) in ein öffentlich erreichbares Verzeichnis wie:

https://mywebpage.de/wp-content/uploads/2025/06/ParameterIdentifikation.sage

HTML-Block einfügen

Füge in deinem Beitrag folgenden Code ein:

<div id="sage-cell-parameter"></div>

<script src="https://sagecell.sagemath.org/static/embedded_sagecell.js"></script>
<script>
fetch("https://mywebpage.de/wp-content/uploads/2025/06/ParameterIdentifikation.sage")
  .then(response => response.text())
  .then(codeContent => {
    sagecell.makeSagecell({
      inputLocation: "#sage-cell-parameter",
      template: "minimal",
      code: codeContent,
      evalButtonText: "Berechnen"
    });
  });
</script>

Hinweise

• Der Code aus der Datei wird sichtbar eingebettet.
• Der Leser kann den Code über den Button „Berechnen“ direkt ausführen.
• Die Methode fetch(...).then(...) stellt sicher, dass der Textinhalt korrekt übertragen wird.

• SageMath findet sich hier und zum Webinterface SageMathCell siehe hier. Auf der SageMathCell-Website finden sich auch eine Beschreibung zur Einbettung in eine Webseite.
• Zugeordnete Legendrepolynome
• Kugelflächenfunktionen
• Parameteridentifikation