Die GWR GmbH entwickelt Algorithmen und entsprechende Software zu Aufgabenstellungen der Angewandten Mathematik und führt Auftragsberechnungen durch. Unsere Kompetenzfelder sind

• Numerische Simulationen
• Mathematische Modelle
• schnelle Lösung großer Gleichungssysteme
• C++-Programmierung, insbesondere
  • Parallelisierungen und Multicore-Anwendungen, MPI, OpenMp und Threading Building Blocks
• Strömungsberechnungen mit OpenFOAM
• Visualisierungen
• Algorithmische Geometrie
  • Massiv parallele Sichtbarkeitsberechnung

• Physics-Informed Neural Networks (PINNs) & Operator Networks (PINOs):
  Moderne Machine-Learning-Modelle, die physikalische Gesetze direkt in neuronale Netze integrieren. PINNs approximieren einzelne Lösungen physikalischer Gleichungen – also Funktionen. PINOs hingegen lernen ganze Lösungsoperatoren, also Abbildungen zwischen Funktionenräumen. Beide Ansätze verbinden datengetriebene Methoden mit physikalischem Vorwissen.
• kombinatorische Optimierung.

Wir nutzen eine Vielzahl von Programmiersprachen und Tools, darunter C++, Lua, Python, Java und Shell-Skripte. Unsere Softwareentwicklungsprozesse werden durch den Einsatz von Git zur Versionsverwaltung und Jenkins zur Automatisierung kontinuierlich optimiert.

Simulationen

Numerische Simulationen kommen in zahlreichen Anwendungsbereichen zum Einsatz – zum Beispiel bei der Strömungssimulation im Automobilbau, bei Finite-Elemente-Analysen zur Berechnung von Spannungen und Verformungen in Bauteilen oder in der Modellierung von Finanzmärkten und Wetterentwicklungen. Grundlage vieler Verfahren sind mathematische Modelle aus der Physik, mit denen sich komplexe Phänomene realitätsnah abbilden lassen. Zunehmend kommen auch Methoden der Künstlichen Intelligenz zum Einsatz, etwa zur Beschleunigung von Berechnungen oder zur Auswertung großer Datenmengen. Simulationen ermöglichen virtuelle Experimente, die zur Entwicklung neuer Produkte oder zur Optimierung technischer Abläufe beitragen – etwa in Wissenschaft, Industrie und Technik.

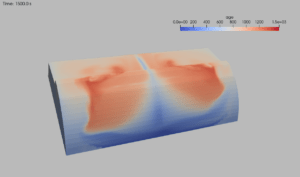
Algorithmen

Eine Problemstellung sollte mit dem “richtigen” Algorithmus gelöst werden, da die Wahl des geeigneten Algorithmus entscheidend für die Effizienz der Lösung ist. Ein eindrucksvolles Beispiel hierfür ist die schnelle Fourier-Transformation[1] (FFT).  Im Vergleich zur direkten Auswertung der trigonometrischen Summenformel bietet sie eine erhebliche Verbesserung. Während die naive Methode \(\mathcal{O}(n^2)\) Rechenschritte benötigt, weist die FFT lediglich einen Aufwand von \(\mathcal{O}(n \log ⁡n)\) auf.

Unser Beispiel zum Modularen Potenzieren verdeutlicht, wie allein durch die Auswahl des Verfahrens eine dramatische Beschleunigung der Laufzeit erzielt werden kann. Von ursprünglich 10 Sekunden reduziert sich die Rechenzeit auf nur wenige Mikrosekunden.

Auch bei der numerischen Lösung der Radiosity-Gleichung zur Berechnung des Energietransports durch Wärmestrahlung sowie in der Parameteridentifikation zeigt sich, wie sehr die Wahl eines geeigneten Algorithmus das Ergebnis beeinflusst – sowohl in Bezug auf Stabilität als auch auf Recheneffizienz.

Programmierung

Software, insbesondere Programme zur Simulation, sollte sich kontinuierlich weiterentwickeln, um das volle Potenzial der verfügbaren Hardware auszuschöpfen. Dabei spielen spezielle Softwaretechniken wie OpenMP und Threading Building Blocks für MultiCore-Architekturen sowie SYCL für plattformübergreifende Programmierung (CPU + GPU) eine entscheidende Rolle. Diese Techniken ermöglichen eine effiziente Nutzung moderner Hardware und tragen dazu bei, die Leistungsfähigkeit von Anwendungen zu maximieren.