Parameteridentifikation: ein klassisches Inverses Problem
Parameteridentifikation ist ein zentrales Thema in der Inversen Theorie. Dabei geht es um die Bestimmung einer unbekannten Funktion. Im Folgenden wird ein typisches Szenario behandelt: die Bestimmung einer unbekannten Parameterfunktion \( \lambda \) aus gegebenen Daten \( y \), die über einen Integraloperator \( \mathcal{A} \) mit \( \lambda \) verknüpft sind. Die zugrunde liegende Operatorgleichung ist linear, das numerische Verfahren basiert auf einer Diskretisierung mittels Trapezregel und der Lösung eines linearen Gleichungssystems.
Die Problemstellung geht auf einen Beitrag von Kirsch[1] im Sammelband Trends in Mathematical Optimization zurück und eignet sich gut, um grundlegende Phänomene inverser Probleme – insbesondere Instabilität, schlechte Konditionierung und die Notwendigkeit von Regularisierung – anschaulich darzustellen. Der Text baut auf einer früheren Version auf. Die vorliegende Fassung präzisiert die Darstellung der adjungierten Abbildung und ihrer konsistenten Diskretisierung und ergänzt sie um einen Vergleich äquivalenter Implementierungen in MATLAB und Python hinsichtlich numerischer Übereinstimmung, Laufzeit und Threadskalierung.
Inhaltsverzeichnis
- Das Problem
- Numerische Lösung der Parameteridentifikation
- Zur Regularisierung
- Zusammenfassung
- Sage-Skript
- Implementierungen mit MATLAB und Python
- Quellen
Das Problem
Gegeben sei
\[
(\mathcal{A}\lambda ) (t) = \int_0^1 \lambda(s) \, e^{ts} \, ds, \qquad t \in [0,1] \tag{1}
\]
Man kann zeigen, dass \(\mathcal A\) injektiv ist. Wenn sich \(y\) in der Form \(y=\mathcal A\lambda\) darstellen lässt, ist die Lösung \(\lambda\) daher eindeutig. Nicht jede beliebige Funktion \(y\in L^2(0,1)\) besitzt jedoch eine solche Darstellung. Der Operator ist somit nicht surjektiv auf \(L^2(0,1)\).
Als konkretes Beispiel sei \( \lambda(t) = e^t \). So ist
\[
y (t) := \mathcal{A} (e^t) = \frac{1}{t+1} \left( e^{t + 1} – 1 \right), \qquad t \in [0,1] \tag{2}
\]
Wir ändern nun den Blickwinkel und betrachten \( \lambda \) als „Parameterfunktion“, die es zu bestimmen gilt, wobei die Kenntnis der Funktion \( y \) aus (2) vorausgesetzt wird. Dazu sei das folgende numerische Verfahren gewählt:
Diskretisierung
- Ersetze das Integral (den Operator \( \mathcal{A} \)) durch die summierte Trapezregel (eine Diskretisierung des Problems).
- Die Unterteilung \( 0 = x_0 < x_1 < \ldots < x_{n-1} < x_n =1 \), \( n > 0 \) führt zu
\[
T_n(f, [0,1]) := \sum_{j=0}^{n-1} \frac{x_{j+1} – x_j }{2} \left( f(x_j) + f(x_{j+1}) \right)
\]
Mit \( x_i = i h \), \( h=1/n \) ist
\[
T_n(f, [0,1]) = \frac{1}{2n} \left( f(0) + f(1) \right) + \frac{1}{n} \sum_{j=1}^{n-1} f(x_j) \tag{3}
\]
und es gilt eine Fehlerabschätzung (\( f \in C^2[0,1] \)) der Form
\[
T_n(f, [0,1]) – \int_0^1 f(s) \, ds = \frac{h^2}{12} f^{(2)}(\xi), \quad \text{für ein } \xi \in (0,1)
\] - Die summierte Trapezregel für (1) lautet demnach
\[
\int_0^1 \lambda(s) \, e^{ts} \, ds \approx \frac{1}{2n} \left( \lambda(0) + \lambda(1) e^{t} \right) + \frac{1}{n} \sum_{j=1}^{n-1} \lambda(x_j) e^{t x_j} \tag{4}
\]
Gesucht sind daher die Funktionswerte von \( \lambda \) in den Stützstellen \( x_i \). Gegeben ist die Funktion \( y \). Zur Bestimmung der \( n+1 \) unbekannten Werte \( \lambda_i := \lambda(x_i) \) haben wir die (semi-diskrete) Gleichung
\[
\frac{1}{2n} \left( \lambda(x_0) + \lambda(x_n) e^{x_i} \right) + \frac{1}{n} \sum_{j=1}^{n-1} \lambda(x_j) e^{x_i x_j} = y(x_i), \quad i=0,\ldots,n
\]
bzw. als lineares Gleichungssystem geschrieben
\[
\mathbf{A}_n \boldsymbol{\alpha} = \mathbf{y} \tag{5}
\]
mit
\[
a_{ij} =
\begin{cases}
\frac{1}{2n} e^{x_i x_j} & j = 0 \text{ oder } j = n \\\\
\frac{1}{n} e^{x_i x_j} & \text{sonst}
\end{cases}
\]
und
\[
\mathbf{y} = \left( y(x_i) \right)_{i=0}^n ,\qquad \boldsymbol{\alpha} = \left( \lambda(x_i) \right)_{i=0}^n
\]
Obwohl der Operator \( \mathcal{A} \) im kontinuierlichen Fall selbstadjungiert ist, ist die Matrix \( \mathbf{A}_n \) im Allgemeinen nicht symmetrisch. Grund dafür sind die unterschiedlichen Gewichte der Trapezregel an den Rändern. Zum Beispiel: \( a_{01} = \frac{1}{n} \), aber \( a_{10} = \frac{1}{2n} \).
Numerische Lösung der Parameteridentifikation
Für verschiedene \( n \) wurde die Kondition der Matrix \( A_n \) bestimmt, das Gleichungssystem (5) aufgestellt und gelöst. \( \alpha(t) \) sei die durch den Vektor \( \alpha \) gegebene stückweise lineare Funktion. Die Kondition, der absolute Fehler \( \| \alpha(t) – e^t \|_\infty \) und der relative Fehler \( \| \alpha(t) – e^t \|_\infty / \| e^t \|_\infty \) sind in Tabelle 1 aufgeführt.
Ergebnisse zum Gleichungssystem (5)
| n | cond(A) | \( \| \alpha – e^t \|_\infty \) | rel. Fehler |
|---|---|---|---|
| 1 | 5.87 | 1.0 | 36.7 % |
| 2 | 168.03 | 1.0388 | 38.2 % |
| 4 | 910021.07 | 1.08964 | 40.0 % |
| 8 | 7.85e+14 | 4.7194 | 173 % |
| 16 | 7.87e+17 | 108.34 | 3985 % |
| 32 | 2.79e+19 | 267.85 | 9853 % |
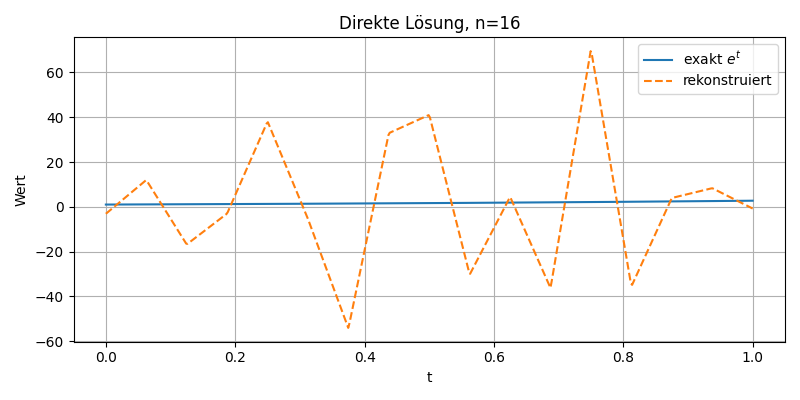
Dieses Diagramm zeigt den Vergleich zwischen der exakten Lösung \( e^t \) (blaue Linie) und der numerisch rekonstruierten Funktion \( \alpha(t) \) (orange gestrichelt) bei direkter Lösung des Gleichungssystems \( \mathbf{A}_n \alpha = y \) mit \( n = 16 \). Aufgrund der schlechten Kondition der Matrix \( \mathbf{A}_n \) ist das Verfahren instabil: Die rekonstruierten Werte oszillieren stark und weichen erheblich vom exakten Verlauf ab. Das Beispiel illustriert die typische Problematik schlecht gestellter inverser Aufgaben und macht die Notwendigkeit einer Regularisierung deutlich.
Zur Regularisierung
Zur Regularisierung des schlecht gestellten Problems wird die Tikhonov-Regularisierung eingesetzt:
\[
(\beta I + \mathcal{A}^* \mathcal{A}) \,\lambda = \mathcal{A}^* y \tag{6}
\]
Dabei bezeichnet \( \mathcal{A}^* \) die adjungierte Abbildung des Operators \( \mathcal{A} \). Sie ist definiert durch die Bedingung:
\[
\langle \mathcal{A} \lambda, y \rangle = \langle \lambda, \mathcal{A}^* y \rangle
\quad\text{für alle } \lambda, y \in L^2(0,1).
\]
Wenn man die Definition von \( \mathcal{A} \) einsetzt, ergibt sich durch Vertauschen der Integrale (Fubini):
\[
(\mathcal{A}^* y)(s) = \int_0^1 e^{t\,s}\,y(t)\,\mathrm{d}t. \tag{7}
\]
Da die Darstellung von \( \mathcal{A}^* \) formal genau der von \( \mathcal{A} \) entspricht (bis auf die Benennung der Integrationsvariable), ist die Aufgabe selbstadjungiert, d.h. \( \mathcal{A}^* = \mathcal{A} \).
Bei der Diskretisierung mit der Trapezregel sind die Randgewichte halbiert, sodass die entstehende Matrix \( \mathbf{A}_n \) nicht symmetrisch ist. Folglich ist die Annahme \( \mathbf{A}_n^* = \mathbf{A}_n^T \) falsch und führt zu Fehlern. Korrekt ist vielmehr, die adjungierte Abbildung ebenso mit der Trapezregel zu diskretisieren, wodurch \( \mathbf{A}_n^* = \mathbf{A}_n \) gilt.
Diskretes Regularisierungssystem (konsistent)
Mit der korrekten adjungierten Matrix \(A_n^* = A_n\) lautet die diskrete Tikhonov-Gleichung
\[
\bigl(\beta\,\mathbf{I} + \mathbf{A}_n\,\mathbf{A}_n\bigr)\,\boldsymbol{\alpha}_\beta
\;=\;\mathbf{A}_n\,\mathbf{y}.
\tag{8a}
\]
Regularisierte Lösung gemäß Gleichung (8a), \( \beta = 10^{-3} \)
| n | \( \| \alpha – e^t \|_\infty \) | rel. Fehler |
|---|---|---|
| 1 | 0.99 | 36.6 % |
| 2 | 0.60 | 22.0 % |
| 4 | 0.234 | 8.6 % |
| 8 | 0.1 | 3.6 % |
| 16 | 0.063 | 2.3 % |
| 32 | 0.054 | 1.9 % |
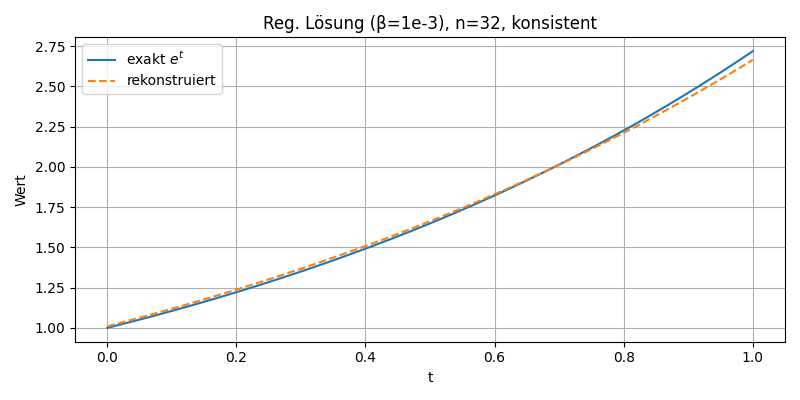
Der Plot zeigt den Vergleich zwischen der exakten Lösung \( e^t \) (blaue Linie) und der numerisch rekonstruierten Funktion (orange gestrichelt) für \( n = 32 \) mit Tikhonov-Regularisierung bei konsistenter Diskretisierung der adjungierten Matrix. Die Annäherung ist bereits recht gut; der maximale Fehler beträgt etwa 2.3 %. Für eine höhere Genauigkeit – etwa unter 0.1 % – müsste \( n \) weiter erhöht (z. B. auf \( n = 128 \)) und der Regularisierungsparameter auf \( \beta = 10^{-6} \) reduziert werden.
Gleichung (8a), \( \beta = 10^{-6} \)
| n | \( \| \alpha – e^t \|_\infty \) | rel. Fehler |
|---|---|---|
| 1 | 1.0 | 36.7 % |
| 2 | 1.0335 | 38.0 % |
| 4 | 0.5639 | 20.7 % |
| 8 | 0.202 | 7.4 % |
| 16 | 0.057 | 2.12 % |
| 32 | 0.016 | 0.6 % |
| 128 | 0.0029 | 0.10 % |
Diskretes Regularisierungssystem (inkonsistent)
Setzt man fälschlich \(A_n^* = A_n^T\), erhält man stattdessen
\[
\bigl(\beta\,\mathbf{I} + \mathbf{A}_n^T\,\mathbf{A}_n\bigr)\,\boldsymbol{\alpha}_\beta
\;=\;\mathbf{A}_n^T\,\mathbf{y}.
\tag{8b}
\]
Effekt einer nicht-konsistenten Diskretisierung (Gleichung (8b))
| n | \( \| \alpha – e^t \|_\infty \) | rel. Fehler |
|---|---|---|
| 1 | 0.99 | 36.6 % |
| 2 | 0.96 | 35 % |
| 4 | 1.0339 | 38 % |
| 8 | 1.19 | 43.9 % |
| 16 | 1.28 | 47.4 % |
| 32 | 1.3371 | 49.18 % |
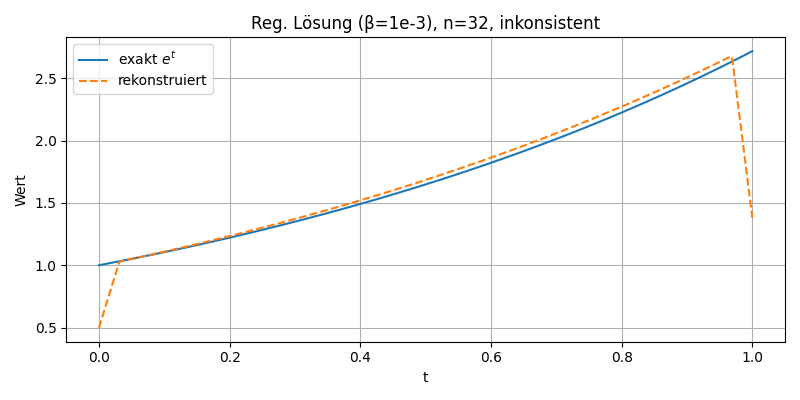
In dieser Darstellung wird die exakte Lösung \( e^t \) (blau) der rekonstruierten Funktion (orange gestrichelt) gegenübergestellt, wobei die Tikhonov-Regularisierung mit inkonsistenter Diskretisierung der adjungierten Matrix verwendet wurde. Trotz Regularisierung zeigen sich deutliche Abweichungen am Rand. Dies unterstreicht die Bedeutung einer konsistenten Diskretisierung bei der Parameteridentifikation.
Zusammenfassung
- Die direkte Lösung des Gleichungssystems (5) ist numerisch instabil. Die Matrix \( \mathbf{A}_n \) ist schlecht konditioniert, was bei wachsendem \( n \) zu stark fehlerhaften Lösungen führt.
- Die Tikhonov-Regularisierung gemäß Modell (8a) stabilisiert das Problem erfolgreich. In Abhängigkeit vom Regularisierungsparameter \( \beta \) und der Diskretisierung \( n \) lässt sich die exakte Parameterfunktion \( \lambda(t) = e^t \) mit hoher Genauigkeit rekonstruieren.
- Eine konsistente Diskretisierung der adjungierten Abbildung \( \mathcal{A}^* \) ist entscheidend. Wird stattdessen fälschlich die transponierte Matrix \( \mathbf{A}_n^T \) verwendet (Modell (8b)), bleibt die Lösung zwar beschränkt, konvergiert jedoch nicht gegen die exakte Funktion \( e^t \).
Sage-Skript
Das Sage-Skript führt die numerische Untersuchung des Modellproblems Parameteridentifikation mit Tikhonov-Regularisierung automatisiert durch. Es erledigt dabei folgende Schritte:
- Aufbau der Diskretisierungsmatrix \(A_n\)
Verwendung der summierten Trapezregel auf \([0,1]\) mit \(n+1\) Stützstellen;
Bildung der Matrixeinträge \(a_{ij}=w_j\,e^{x_i x_j}\). - Berechnung der Konditionszahl
Bestimmung der größten und kleinsten Singulärwerte mittels NumPy;
Kennzahl \(\kappa(A_n)=\sigma_{\max}/\sigma_{\min}\). - Direkte Lösung
Lösung des linearen Systems \(A_n\,\alpha=y\) für \(\alpha\);
Berechnung des absoluten und relativen Fehlers gegenüber \(\lambda(t)=e^t\). - Tikhonov-Regularisierung
Lösen von \((\beta I + A_n^*A_n)\,\alpha_\beta = A_n^*y\) mit
konsistent: \(A_n^*=A_n\)
inkonsistent: \(A_n^*=A_n^T\)
Vergleich der Regularisierungsergebnisse für \(\beta=10^{-3}\) (Modell 1) und \(\beta=10^{-6}\) (Modell 2). - Ausgabe
Fünf einheitliche Tabellen im ASCII-Format:- Direkte Lösung (ohne Regularisierung)
- Modell 1 (konsistent / inkonsistent)
- Modell 2 (konsistent / inkonsistent)
Implementierungen mit MATLAB und Python
Motivation
Den Anstoß für diese Erweiterung gab eine praktische Frage aus dem wissenschaftlichen Rechnen: Wie lässt sich ein vorhandenes numerisches Modell von MATLAB nach Python übertragen, ohne seine mathematische Aussage oder seine numerische Qualität zu verändern?
Eine solche Portierung ist keine reine Sprachfrage. Zuerst muss geklärt werden, ob beide Programme wirklich dasselbe mathematische Modell, dieselbe Diskretisierung und dieselben Rand- beziehungsweise Quadraturbehandlungen verwenden. Erst danach sind Aussagen über numerische Übereinstimmung, Wartbarkeit oder Geschwindigkeit sinnvoll.
Das Modellproblem dieses Beitrags bietet dafür einen überschaubaren Referenzfall. Ausgehend vom vorangehenden Sage-Skript diskretisieren die neuen MATLAB- und Python-Fassungen denselben Integraloperator und lösen dieselben direkten beziehungsweise regularisierten Gleichungssysteme. Der Vergleich konzentriert sich auf zwei Fragen: Stimmen die numerischen Ergebnisse überein, und wie unterscheiden sich Laufzeit und Speicherbedarf der konkreten Implementierungen?
Für kleine und mittlere Diskretisierungen steht die mathematische Validierung im Vordergrund. Große Matrizen werden ausschließlich als Performance- und Skalierungstest verwendet, da die direkte inverse Aufgabe mit wachsendem n extrem schlecht konditioniert ist.
Gemeinsame diskrete Referenz
Alle drei Implementierungen verwenden die äquidistanten Stützstellen \(x_i=i/n\), \(i=0,\ldots,n\), und die Gewichte der summierten Trapezregel. Mit
\[
K_{ij}=\exp(x_i x_j),
\qquad
W=\operatorname{diag}(w_0,\ldots,w_n),
\qquad
A=KW
\]
lautet die direkte diskrete Aufgabe
\[
A\boldsymbol{\alpha}=\boldsymbol{y}.
\]
Die konsistent diskretisierte Tikhonov-Gleichung wird in allen Programmen in derselben Form gelöst:
\[
(\beta I+A A)\boldsymbol{\alpha}_{\beta}=A\boldsymbol{y}.
\]
Damit vergleichen wir tatsächlich dieselbe mathematische Aufgabe. Insbesondere darf die diskrete adjungierte Abbildung hier nicht stillschweigend durch die gewöhnliche transponierte Matrix ersetzt werden; die Quadraturgewichte müssen konsistent berücksichtigt bleiben.
MATLAB-Implementierung
Die MATLAB-Fassung bildet Stützstellen, Quadraturgewichte und Matrix vektorisiert und verwendet die lineare Algebra des installierten MATLAB-Backends. Direkte und regularisierte Lösung werden getrennt ausgewertet, damit Konditionierung, Rekonstruktionsfehler und Laufzeit nicht miteinander vermischt werden.
% Diskretisierung und konsistente Tikhonov-Regularisierung
n = 32;
beta = 1.0e-6;
x = (0:n).'/n;
weights = ones(n+1, 1)/n;
weights([1, end]) = 1/(2*n);
A = exp(x*x.').*weights.';
y = expm1(x+1)./(x+1);
lambdaExact = exp(x);
conditionA = cond(A, 2);
alphaDirect = A\y;
directError = max(abs(alphaDirect-lambdaExact));
lhs = beta*eye(n+1) + A*A;
rhs = A*y;
alphaRegularized = lhs\rhs;
regularizedError = max(abs(alphaRegularized-lambdaExact));Beim Matrixaufbau bezeichnet .* die elementweise Multiplikation des Kerns mit den Quadraturgewichten. Die Produkte A*A und A*y sind dagegen gewöhnliche Matrixprodukte.
Python-/NumPy-Implementierung
Die Python-Fassung verwendet NumPy und folgt derselben Reihenfolge von Matrixaufbau, direkter Lösung und Tikhonov-Regularisierung. Für einen fairen Vergleich werden keine sprachspezifischen Vereinfachungen verwendet, die das mathematische Verfahren verändern würden.
# Diskretisierung und konsistente Tikhonov-Regularisierung
import numpy as np
n = 32
beta = 1.0e-6
x = np.arange(n + 1, dtype=np.float64) / n
weights = np.full(n + 1, 1.0 / n, dtype=np.float64)
weights[[0, -1]] = 1.0 / (2.0 * n)
A = np.exp(np.outer(x, x)) * weights[np.newaxis, :]
y = np.expm1(x + 1.0) / (x + 1.0)
lambda_exact = np.exp(x)
condition_A = np.linalg.cond(A)
alpha_direct = np.linalg.solve(A, y)
direct_error = np.max(np.abs(alpha_direct - lambda_exact))
lhs = beta * np.eye(n + 1) + A @ A
rhs = A @ y
alpha_regularized = np.linalg.solve(lhs, rhs)
regularized_error = np.max(np.abs(alpha_regularized - lambda_exact))NumPy verwendet * für die elementweise Multiplikation und @ für Matrixprodukte. Abgesehen von diesen syntaktischen Unterschieden führen beide Listings dieselben Rechenschritte in derselben Reihenfolge aus.
Als Referenz dienen die Ergebnisse des vorangehenden Sage-Abschnitts. Die neue Gegenüberstellung prüft, ob MATLAB und Python diese Referenzfälle reproduzieren.
Numerische Übereinstimmung
Zunächst werden kleine und mittlere Werte von n untersucht. Bei der direkten Lösung sind nur die noch ausreichend stabilen Fälle bis \(n=4\) für einen Vergleich der Implementierungen geeignet. Für feinere Gitter werden die regularisierten Rekonstruktionsfehler gegenüber \(\lambda(t)=\exp(t)\) verglichen.
| Verfahren | n | Sage | MATLAB/Python |
|---|---|---|---|
| direkt | 1 | 1.0 | 1.0000 |
| direkt | 2 | 1.0388 | 1.0388 |
| direkt | 4 | 1.08964 | 1.0896 |
| \(\beta=10^{-3}\) | 4 | 0.234 | 0.23438 |
| \(\beta=10^{-3}\) | 8 | 0.1 | 0.10021 |
| \(\beta=10^{-3}\) | 16 | 0.063 | 0.063559 |
| \(\beta=10^{-3}\) | 32 | 0.054 | 0.054207 |
| \(\beta=10^{-6}\) | 4 | 0.5639 | 0.56395 |
| \(\beta=10^{-6}\) | 8 | 0.202 | 0.20214 |
| \(\beta=10^{-6}\) | 16 | 0.057 | 0.057867 |
| \(\beta=10^{-6}\) | 32 | 0.016 | 0.016412 |
| \(\beta=10^{-6}\) | 128 | 0.0029 | 0.0029506 |
MATLAB und Python reproduzieren die stabilen direkten Fälle und die veröffentlichten regularisierten Sage-Werte. In allen aufgeführten Fällen liefern sie auf die dargestellten fünf signifikanten Stellen dieselben Maximalfehler. Beim feinsten gezeigten Fall mit \(n=128\) und \(\beta=10^{-6}\) unterscheiden sich die ungerundeten Ergebnisse lediglich um ungefähr \(10^{-9}\).
Bei der direkten Lösung steigt die Konditionszahl dagegen bereits von ungefähr \(9.1\cdot10^5\) für \(n=4\) auf etwa \(7.9\cdot10^{14}\) für \(n=8\). Ab diesem Bereich können verschiedene BLAS-/LAPACK-Backends deutlich unterschiedliche Lösungsvektoren liefern, obwohl sie dieselbe diskrete Matrix verarbeiten. Diese Abweichung ist ein Symptom der Schlechtgestelltheit und kein belastbarer Geschwindigkeits- oder Qualitätsvergleich zwischen den Programmiersprachen.
Laufzeitvergleich
Für den Laufzeitvergleich werden Matrixaufbau, direkte Lösung, Aufbau des Tikhonov-Systems und regularisierte Lösung getrennt gemessen. Die Gesamtzeit ist der Median der Summe dieser vier Phasen pro Lauf. Nicht enthalten sind Programmstart, Paketinstallation und Datei-Ein-/Ausgabe.
| n | N=n+1 | MATLAB [ms] | Python [ms] | Python/MATLAB |
|---|---|---|---|---|
| 64 | 65 | 0.260 ± 0.005 | 0.108 ± 0.000 | 0.42 |
| 128 | 129 | 0.640 ± 0.002 | 0.393 ± 0.001 | 0.61 |
| 256 | 257 | 2.480 ± 0.005 | 2.498 ± 0.003 | 1.01 |
| 512 | 513 | 12.806 ± 0.013 | 14.206 ± 0.033 | 1.11 |
| 1024 | 1025 | 73.044 ± 0.083 | 76.705 ± 0.158 | 1.05 |
Bei den sehr kleinen Matrizen dominieren Aufruf- und Verwaltungsanteile; Python ist dort in dieser Messung schneller. Für \(n=256\) sind beide Gesamtlaufzeiten praktisch gleich. Bei \(n=512\) liegt MATLAB um etwa 11 % und bei \(n=1024\) um etwa 5 % vorn.
| Phase bei n=1024 | MATLAB [ms] | Python [ms] | Python/MATLAB |
|---|---|---|---|
| Matrixaufbau | 7.265 | 4.746 | 0.65 |
| direkte Lösung | 20.203 | 21.406 | 1.06 |
| Aufbau des Tikhonov-Systems | 26.521 | 29.740 | 1.12 |
| regularisierte Lösung | 19.251 | 20.771 | 1.08 |
Die Phasenmessung zeigt ein differenziertes Bild: NumPy baut die Matrix schneller auf, während MATLAB bei den drei Operationen der dichten linearen Algebra moderat vorn liegt. Die Messwerte vergleichen deshalb nicht abstrakt „MATLAB gegen Python“. Ein wesentlicher Teil der Rechenzeit entfällt auf optimierte BLAS- und LAPACK-Bibliotheken. Das Ergebnis beschreibt die getesteten Programme immer zusammen mit ihren numerischen Backends.
Reproduzierbarkeit
- identische Problemdefinition und identische Eingabedaten,
- Matrixdimension \(N=n+1\) ausdrücklich angegeben,
- MATLAB-, Python-, NumPy- und Sage-Version dokumentiert,
- BLAS-/LAPACK-Backend dokumentiert,
- Threadzahl und CPU-Affinität kontrolliert,
- Warm-up vor der Messung,
- mehrere Wiederholungen mit Median und Streuung,
- Validierungs- und Performancefälle getrennt ausgewiesen.
| Messdatum | 14. August 2026 |
|---|---|
| Host | turing |
| CPU | 2 × Intel Xeon Silver 4316, je 20 Kerne, 80 logische CPUs |
| Betriebssystem | Linux 5.14.0, x86-64, glibc 2.34 |
| MATLAB | R2026a Update 4 |
| MATLAB-Backend | Intel oneAPI MKL 2025.0.1, LAPACK 3.11.0 |
| Python | CPython 3.13.14 |
| NumPy | 2.5.2 |
| NumPy-Backend | OpenBLAS 0.3.34, ILP64, Haswell/AVX-512 |
| Threadmodus | ein Rechenthread, Prozess an logische CPU 0 gebunden |
| Wiederholungen | fünf unabhängige Läufe; Python intern jeweils neun Messungen nach einem Warm-up |
MATLAB wurde mit -singleCompThread gestartet. Für Python waren OPENBLAS_NUM_THREADS=1, OMP_NUM_THREADS=1 und MKL_NUM_THREADS=1 gesetzt. Beide Prozesse liefen mit taskset -c 0 auf demselben logischen CPU-Kern.
Der Einthreadmodus wurde bewusst als klar definierte Vergleichsbasis gewählt. Dadurch dominieren unterschiedliche automatische Threadstrategien von MKL und OpenBLAS die Messung nicht. Eine separate Messreihe untersucht im Folgenden die Parallelskalierung mit identischer Threadzahl und kontrollierter CPU-Affinität.
Threadskalierung auf physischen Kernen
Für die Threadmessung wird die dichte Performanceaufgabe auf \(n=8192\), also \(N=8193\), vergrößert. Gemessen werden 1, 2, 4, 8, 16, 20 und 40 Rechenthreads in jeweils fünf unabhängigen Läufen. Bis 20 Threads liegen alle verwendeten physischen Kerne auf dem ersten CPU-Sockel. Der 40-Thread-Punkt verwendet die 40 physischen Kerne beider Sockel. Hyperthreading bleibt vollständig ausgeschlossen.
Die Parallelisierung wird nicht im Modellcode mit parfor oder multiprocessing programmiert. MATLAB begrenzt seine Rechenthreads mit maxNumCompThreads; bei Python steuert OPENBLAS_NUM_THREADS das OpenBLAS-Backend. taskset bindet beide Prozesse an dieselben physischen CPUs. Matrixprodukte und lineare Löser werden damit innerhalb von MKL beziehungsweise OpenBLAS parallel ausgeführt.
MATLAB, Beispiel mit 16 Threads:
taskset -c 0-15 matlab -batch "maxNumCompThreads(16); ..."
Python/NumPy, Beispiel mit 16 Threads:
OPENBLAS_NUM_THREADS=16 OMP_NUM_THREADS=16 MKL_NUM_THREADS=16 \
taskset -c 0-15 python -m gwr_parameteridentifikation.benchmark ...| Threads | MATLAB [s] | Speedup | Effizienz | Python [s] | Speedup | Effizienz |
|---|---|---|---|---|---|---|
| 1 | 24.598 ± 0.005 | 1.00 | 100.0 % | 23.099 ± 0.008 | 1.00 | 100.0 % |
| 2 | 12.778 ± 0.015 | 1.93 | 96.3 % | 12.348 ± 0.005 | 1.87 | 93.5 % |
| 4 | 7.451 ± 0.035 | 3.30 | 82.5 % | 6.917 ± 0.009 | 3.34 | 83.5 % |
| 8 | 4.709 ± 0.006 | 5.22 | 65.3 % | 4.640 ± 0.009 | 4.98 | 62.2 % |
| 16 | 4.016 ± 0.011 | 6.12 | 38.3 % | 4.493 ± 0.006 | 5.14 | 32.1 % |
| 20 | 4.070 ± 0.017 | 6.04 | 30.2 % | 4.630 ± 0.016 | 4.99 | 24.9 % |
| 40 | 3.932 ± 0.058 | 6.26 | 15.6 % | 6.770 ± 0.095 | 3.41 | 8.5 % |
Ergebnisse der Threadskalierung
Bis acht Threads skalieren beide Backends ähnlich und erreichen ungefähr den fünffachen Durchsatz. Danach sättigen die Faktorisierungen und Löser: 20 Threads sind in beiden Implementierungen geringfügig langsamer als 16. NumPy erreicht seine kürzeste Gesamtzeit deshalb bei 16 Threads.
Der MATLAB-Gesamtwert sinkt bei 40 Threads noch knapp unter den 16-Thread-Wert. Die Phasenmessung zeigt jedoch, dass dieser kleine Gewinn ausschließlich aus dem schnelleren Aufbau des Tikhonov-Systems stammt; direkte und regularisierte Lösung werden auf zwei Sockeln wieder langsamer. Bei Python/OpenBLAS überwiegen diese Kosten deutlich, sodass 40 Threads die Gesamtzeit gegenüber 16 Threads um etwa 51 % erhöhen.
Auch der Matrixaufbau reagiert unterschiedlich: MATLAB parallelisiert den vektorisierten Aufbau in dieser Konfiguration sichtbar, während NumPys outer/exp-Folge nahezu einthreadig bleibt. Der 40-Kern-Fall lief unter der Standard-NUMA-Policy von Linux und ist als eigener Zwei-Sockel-Messpunkt zu lesen. Die Skalierungskurve bestätigt damit, dass die konkrete Backend- und Speicherarchitektur wichtiger ist als die bloße Angabe einer maximalen Threadzahl.
Was der Vergleich zeigt
MATLAB und Python können dieselbe Parameteridentifikation mit praktisch übereinstimmenden Resultaten abbilden. Entscheidend für die fachliche Qualität sind jedoch eine konsistente Diskretisierung, eine geeignete Regularisierung und eine sachgerechte Beurteilung der Kondition des diskretisierten Problems. Die Wahl der Programmiersprache beeinflusst Bedienung und konkrete Laufzeit, ändert aber nichts an der mathematischen Schlechtgestelltheit.
Bei großen Diskretisierungen zeigt sich außerdem, dass die Wahl des Algorithmus wesentlich mehr bewirken kann als der Wechsel zwischen MATLAB und Python. Der Kern \(\exp(x_i x_j)\) besitzt eine separierbare Entwicklung. Dadurch lässt sich die vollständige Kernmatrix durch voll besetzte Faktormatrizen mit nur wenigen Spalten darstellen.
Ausblick: Niedrigrangrechnung ohne vollständige Matrix
Die daraus entstehende Niedrigrangrechnung mit separierbaren Kernen ist ein eigenständiges Thema. Im vorliegenden Beispiel ersetzen voll besetzte Faktormatrizen mit nur wenigen Spalten die vollständige Kernmatrix. Damit folgt die Rechnung derselben strukturorientierten Grundidee, die auch hierarchischen Matrizen und dem Panel Clustering zugrunde liegt: Die Darstellung speichert nicht alle Matrixeinträge einzeln, sondern bildet die Operatorwirkung aus kompakten Faktoren.
Hinweis: Die ergänzten Abschnitte zu Sage, MATLAB und Python sowie zur Threadskalierung wurden mit Unterstützung KI-gestützter Werkzeuge ausgearbeitet. Mathematische Aussagen, Implementierungen und Messergebnisse wurden fachlich geprüft und durch reproduzierbare Rechnungen validiert.
Quellen
- (1988): Inverse Problems. In: Hoffmann, K. H.; Hoppe, R. H. W. (Hrsg.): Trends in Mathematical Optimization, S. 117–137, Birkhäuser, Basel, 1988.
Erstellt von Dr. Frank Liebau, Erstfassung: 17. März 2001. Übersetzt in modernes HTML/MathJax 2025.