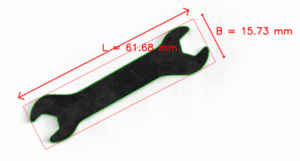
Einleitung
Die Idee, einen Scanner als Messinstrument zu verwenden, entstand eher zufällig. Konkret handelt es sich um einen handelsüblichen Flachbettscanner in einem Multifunktionsdrucker, also kein Spezialgerät. In meinem Fall stehen mir zwei Geräte in der Preisklasse von etwa 200 bis 300 Euro zur Verfügung: ein älteres Modell von HP und ein neueres von Epson. Trotz dieser einfachen Ausstattung eröffnen sich bei flachen Objekten interessante Möglichkeiten in der technischen Vermessung.
Testfall: kleiner Maulschlüssel. OBB (rot), Kontur (grün)
- Geometriemodelle für Simulationen: z. B. Profile von Fensterrahmen als Ausgangspunkt für die Gittererzeugung.
- Qualitätskontrolle: Außenmaße, Lochpositionen oder Beschriftungen automatisiert erfassen und mit Referenzen abgleichen.
Flachbettscanner liefern hochaufgelöste, flächige Aufnahmen unter konstanten Bedingungen: gleichmäßige Beleuchtung, definierte Geometrie und eine bekannte Abtastauflösung (DPI). Damit wird aus einem Alltagsgerät ein praktikables Messinstrument im Zehntelmillimeterbereich.
Für die algorithmische Umsetzung setzen wir auf OpenCV (Python/C++). Kern ist die Konturerkennung, die je nach Strategie entweder auf Schwellwertverfahren nach Otsu (Masken-Modus mit cv2.findContours) oder auf dem Kantenoperator nach Canny (Edge-Modus mit cv2.Canny) basiert.
Aktuell nutzen wir den Masken-Modus: Ein Otsu-Schwellwert erzeugt eine Binärmaske, kleine Störungen werden entfernt, und aus der größten zusammenhängenden Komponente wird die Kontur bestimmt. Daraus ergeben sich zwei zentrale Ergebnisse: die orientierte Bounding-Box (OBB) als kompaktes Maß für Länge, Breite und Winkel, sowie die vollständige Konturlinie, die mit einer definierten Referenzgeometrie verglichen werden kann. Auf dieser Basis ist eine Auswertung der Abweichungen zwischen Ist-Scan und Soll-Modell möglich.
Parallel dazu ist ein Edge-Modus implementiert, der auf dem Canny-Kantenoperator aufsetzt und bei schwierigen Objekten stabilere Ergebnisse verspricht. Dieser Modus wird in einem späteren Beitrag systematisch untersucht.
Kalibrierung des Scanners als Messinstrument: von Pixeln zu Millimetern
Ein digitaler Scan liefert zunächst nur Pixelkoordinaten. Für eine verlässliche Geometriemessung müssen diese in metrische Einheiten umgerechnet werden. Der naheliegende Ansatz ist die Nutzung der im Scanner eingestellten Auflösung in dpi (dots per inch):
$$1\ \text{inch} = 25{,}4\ \text{mm}, \quad
\text{mm pro Pixel} = \tfrac{25{,}4}{\text{dpi}}$$
Beispiel: Bei 600 dpi entspricht ein Pixel ca. 0,0423 mm.
Allerdings ist die nominelle dpi-Angabe nicht immer zuverlässig: Scanner können geringfügige Anisotropien (unterschiedliche Skalierung in x- und y-Richtung) oder systematische Abweichungen aufweisen. Deshalb empfiehlt sich eine praktische Kalibrierung mit Referenzmarken.
Markerbasierte Kalibrierung
Für die Kalibrierung nutzen wir ArUco-Marker – schwarz-weiße Quadrate mit codiertem Innenmuster, die sich robust erkennen lassen und in OpenCV nativ unterstützt sind (cv2.aruco). In unserem Referenz-PDF sind vier Marker in den Ecken angeordnet, mit definierten Abständen (z. B. 150 mm horizontal, 200 mm vertikal). Damit entsteht ein Rechteck fester Größe, das unabhängig vom Papierformat reproduzierbar ist.
Aus den Pixelkoordinaten der Markerzentren wird eine affine Abbildung bestimmt:
-
A– 2×2-Matrix für Maßstab und Scherung, -
b– Verschiebungsvektor, -
sx,sy– effektive mm/px-Skalen entlang der Bildachsen (zur Diagnose).
Die Abbildung wirkt direkt auf die Pixelkoordinaten (x, y) des Scans und liefert die entsprechenden metrischen Koordinaten (X, Y) in Millimetern:
$$
\begin{bmatrix} X \\ Y \end{bmatrix}
= A \cdot \begin{bmatrix} x \\ y \end{bmatrix} + b,
\quad
A \in \mathbb{R}^{2 \times 2},\; b \in \mathbb{R}^2
$$
Alle Pixelkoordinaten des Scans werden damit nach Millimetern transformiert. Das Verfahren gleicht Anisotropien, Versatz und kleine Schiefstellungen aus und ermöglicht eine konsistente metrische Auswertung der Konturen und Maße.
Der Vorteil liegt in der automatisierten Erkennung: Bei jedem Scan werden die Marker erneut detektiert, sodass systematische Abweichungen des Scanners automatisch kompensiert werden. In der Praxis genügt es, ein einmal erzeugtes Marker-PDF in Originalgröße (100 %) auszudrucken. Dabei schneiden wir in der Mitte ein Fenster aus, in das das Prüfteil eingelegt wird. So ist sichergestellt, dass es immer im definierten Bereich zwischen den Markern liegt. Im Programm wird dazu ein entsprechendes ROI (Region of Interest) ausgewählt, das innerhalb des Marker-Rahmens liegt, damit bleibt die Kalibrierung stabil und reproduzierbar.
Konturerkennung und orientierte Bounding-Box (OBB)
Nach der Kalibrierung folgt die Bestimmung der Objektgeometrie: Aus dem Scan wird zunächst ein Binärbild gewonnen (Otsu-Schwelle oder alternativ Canny-Kanten). Daraus extrahiert das Programm die größte zusammenhängende Kontur und berechnet die orientierte Bounding-Box (OBB). Beides wird mit der zuvor bestimmten affinen Abbildung (A, b) von Pixel- in Millimeterkoordinaten transformiert. Neben den reinen Außenmaßen ermöglicht die vollständige Kontur auch den Abgleich mit einem zuvor definierten Designmodell – Abweichungen lassen sich so automatisch auswerten.
Kerncode (Python/OpenCV)
def main():
gray = cv2.imread("scan.jpeg", cv2.IMREAD_GRAYSCALE)
# 1) Affine Kalibrierung über ArUco-Marker
calib = get_affine_from_aruco(gray)
A, b = calib["A"], calib["b"]
# 2) Kontur bestimmen (Masken-Modus: Otsu + Morphologie)
cnt = find_main_contour(gray)
# 3) OBB in mm
box, angle, (W_mm, H_mm) = obb_mm_from_cnt_affine(cnt, A)
# 4) Vergleich mit Designkontur
design = load_design_poly_mm()
stats = compare_contours(cnt, design, A, b)
print(f"L={W_mm:.2f} mm H={H_mm:.2f} mm ∠={angle:.1f}°")
print(f"Abweichung zum Design: RMS={stats['rms']:.3f} mm")
Hinweise:
-
get_affine_from_aruco(gray): liefert die Abbildungp_px → A·p_px + b(px → mm). -
find_main_contour(gray): erzeugt ein Binärbild (Otsu) und wählt die größte Komponente. -
obb_mm_from_cnt_affine: bestimmt die OBB und rechnet direkt in Millimeter um. -
compare_contours: vergleicht Scan-Kontur mit der Soll-Geometrie, z. B. über ein robustes Point-to-Curve-Maß.
Ergebnis
- Kontur und OBB liefern die geometrische Basis für Maße, Flächen und Abstandsanalysen.
- Über den direkten Vergleich mit einem Designmodell werden Abweichungen quantifiziert (z. B. RMS-Fehler oder Seitenversatz).
- Die gesamte Auswertung erfolgt in Millimetern durch die affine Marker-Kalibrierung.
Soll/Ist-Abgleich und Feinausrichtung
Nachdem wir die orientierte Bounding-Box (OBB) bestimmt haben, liegt bereits eine erste Lage des Objekts vor: Verschiebung und Rotation in der Scanner-Ebene. Diese Startlage nutzen wir als Ausgangspunkt für den Abgleich mit einem vorher definierten Design.
Dazu transformieren wir die Scan-Kontur in Millimeterkoordinaten und vergleichen sie direkt mit der Referenzkontur. Anschließend verfeinern wir die Lage mit dem Verfahren refine_pose_p2c unter SciPy. Dabei minimiert der Optimierer ein funktionales Maß für den mittleren Abstand zwischen Scan-Kontur und Design.
# Startlage aus OBB
theta0 = _pose_from_obb_mm(px_to_mm(box, A, b))
print(f"[Start] tx={theta0[0]:+.3f} mm ty={theta0[1]:+.3f} mm phi={theta0[2]:+.2f}°")
# Feinausrichtung mit SciPy (Powell-Minimierung)
theta_hat, info = refine_pose_p2c(
design_mm=design,
scan_mm=cnt_mm,
theta0=theta0,
window_mm=8.0, angle_window_deg=6.0,
ds_design_mm=0.5, ds_scan_mm=0.5,
loss="huber", delta=0.2
)
print(f"[Optimiert] tx={theta_hat[0]:+.3f} mm ty={theta_hat[1]:+.3f} mm phi={theta_hat[2]:+.2f}°")
print(f"[Score] Abstand (RMS) = {info['score']:.3f} mm")
Das Ergebnis ist eine Lagebestimmung, bei der die Abweichungen zwischen Scan und Design quantifiziert werden. Neben dem RMS-Fehler stehen weitere Kennwerte (z. B. Perzentile oder Maximalabweichungen) zur Verfügung, sodass sich die Abweichung vom Soll bewerten lässt.
Beispiel: Bankkarte (ID-1-Format)
Als Referenzobjekt eignet sich eine Giro-/Kreditkarte im ID-1-Format (ISO/IEC 7810). Das Sollmaß beträgt 85,60 × 53,98 mm. Die zulässigen Toleranzen liegen bei +0,12/−0,13 mm in der Länge und +0,05/−0,06 mm in der Breite. Ausgewertet wurden vier Scans (Nr. 13–16) bei unveränderter Lage.
Die nachfolgende Tabelle fasst vier Scans derselben Bankkarte (ID-1) zusammen. Länge und Breite stammen aus der Mittelzone; der RMS-Fit gibt den mittleren Soll-Ist-Abstand der Konturen an.
| Scan | Länge [mm] | Breite [mm] | ΔL [mm] | ΔB [mm] | RMS-Fit [mm] |
|---|---|---|---|---|---|
| #13 | 85.863 | 54.076 | +0.263 | +0.096 | 0.046 |
| #14 | 85.867 | 54.074 | +0.267 | +0.094 | 0.047 |
| #15 | 85.863 | 54.073 | +0.263 | +0.093 | 0.045 |
| #16 | 85.860 | 54.072 | +0.260 | +0.092 | 0.045 |
Fazit und Ausblick
Die Breite der Karte liegt sehr nah am Soll (ΔB ≈ +0,09 mm). In der Länge bleibt ein konsistenter Offset (ΔL ≈ +0,26 mm), der bei den gezeigten Scans vor allem durch einen leichten Schatten- bzw. Halo-Effekt an den Stirnseiten entsteht. Dieser verschiebt die ermittelte Kante minimal „nach außen“ und wirkt sich damit auf das Längenmaß stärker aus als auf die Breite.
Zur weiteren Verbesserung bieten sich mehrere Hebel an: Beim Scannen ein dunkler Hintergrund statt Weiß und, wo möglich, eine höhere Auflösung (z. B. 1200 dpi) sowie verlustfreie Formate (TIFF statt JPEG). Algorithmisch prüfen wir den Edge-Modus mit dem Canny-Kantenoperator, um Kanten robuster gegen Schatten zu trennen. Ergänzend könnte auch eine kleine, gerätespezifische Offset-Kompensation auf Basis von Referenzscans hinterlegt werden. Ein weiterer Ansatz ist die Kalibrierung mit allen vier Markern: Statt nur drei Marker zur eindeutigen Bestimmung der affinen Abbildung \(A, b\) zu verwenden, erlaubt die Nutzung aller Ecken eine Überbestimmung und damit eine robustere Least-Squares-Anpassung. Zusammen mit modernerer Hardware sollte sich so die Messunsicherheit weiter reduzieren.