Kugelflächenfunktionen sind mathematische Funktionen, die auf der Oberfläche einer Kugel definiert sind. Als Eigenfunktionen des Laplace-Operators spielen sie eine wichtige Rolle bei der Lösung partieller Differentialgleichungen und werden daher oft als Ansatzfunktionen verwendet. Mithilfe von Kugelflächenfunktionen lässt sich die räumliche Verteilung von Strahlung, Schall oder elektrischen Feldern in einer kugelförmigen Umgebung beschreiben, zum Beispiel die Verteilung von Gravitations- oder Magnetfeldern auf der Erde.
Ähnlich der diskreten Fouriertransformation gibt es auch für die Kugelflächenfunktionen einen schnellen Algorithmus, bekannt als Fast Spherical Harmonic Transform (FSHT). Dieser Algorithmus ermöglicht die effiziente Berechnung der Kugelflächenkoeffizienten aus den Daten einer sphärischen Funktion.
Basisfunktionen
Gautron[1] stellt eine Basis aus Kugelflächenfunktionen für die Hemisphäre vor. Durch die Transformation \(x \rightarrow 2\, x-1\), können Kugelflächenfunktionen auf der Halbkugel erklärt werden.
Seien \(l \in \mathbb{N}\), \(m \in \mathbb{Z}\) mit \(|m| \leq l\), \(\phi \in [0,2\pi)\) der Azimutwinkel und \(\theta \in [0, \pi/2]\) der Polarwinkel.
$$
H_l^m: \, [0, \frac{\pi}{2}]\times [0,2\pi) \rightarrow \mathbb{R} , \quad H_l^m(\theta, \phi) := \begin{cases}
\sqrt{2} \, K_l^m \, \cos( m\, \phi) \, \widetilde{P}_l^m( \cos \theta ) & \quad \text{für } m > 0 \\
\sqrt{2} \, K_l^m \, \sin( |m| \, \phi) \, \widetilde{P}_l^{|m|}( \cos \theta ) & \quad \text{für } m < 0 \\ K_l^0 \, \widetilde{P}_l^0( \cos \theta ) & \quad m = 0 \\ \end{cases}
$$
wobei
$$
\widetilde{P}_l^m( x ) = P_l^m(2\, x-1), \quad x\in [0,1]
$$
die geshifteten assoziierte Legendre-Funktionen, (siehe auch hier) und
$$
K_l^m= \sqrt{ \frac{(2\,l+1)}{ 2 \, \pi } \frac{(l-|m|)!}{(l+|m|)!} }
$$ Normierungsfaktoren sind. Insbesondere ist
$$
K_l^0= \sqrt{ \frac{2\,l+1}{ 2 \, \pi } }, \qquad K_l^m = K_l^{-m}.
$$ Die Funktionen \(H_l^m\) werden als hemispherical harmonics, kurz HSH, bezeichnet.
- Die Ansatzfunktionen werden durch das Paar \((l,m)\) indiziert, wobei \(l\) den Grad und \(m\) die Ordnung angibt.
- Die HSHs sind othonormal: $$ \newcommand{\Spro}[2]{\langle {#1},{#2} \rangle} \Spro{H_l^m}{H_k^n}_{\mathcal{H}^2}:= \int_{\mathcal{H}^2} H_l^m(\theta, \phi) \, H_k^n(\theta, \phi) d\omega = \delta_{lk}\delta_{mn} .$$ Dabei bezeichnet \(\mathcal{H}^2 := [0, \pi/2]\times [0,2\pi] \) die Halbkugel.
$$
\mathcal{I}_{\omega}(n) := \{ (l,m) \, : \, l \in \mathbb{N} , m\in \mathbb{Z}, \text{ mit } l \leq n, \; |m|\leq n \} .
$$
Ein Ansatz (wie hier) über die ersten \(n+1\) Bänder enthält insgesamt \((n+1)^2\) Basisfunktionen \(H_l^m\), d.h. \(|\mathcal{I}_{\omega}(n)| = (n+1)^2.\)
Reihenentwicklung
Sei \(f: \mathcal{H}^2 \rightarrow \mathbb{R}\) eine quadratintegrierbare Funktion. Dann gilt
$$
f(\theta, \phi) = \sum_{l=0}^\infty \sum_{m=-l}^l f_{l}^m \, H_l^m(\theta, \phi)
$$
mit den Entwicklungskoeffizienten
$$
f_{l}^m = \Spro{f}{H_l^m}_{\mathcal{H}^2} = \int_0^{\pi/2} \int_0^{2\, \pi} f(\theta,\phi) \, H_l^m(\theta, \phi) \, d\phi \,\sin(\theta) \, d\theta .
$$
Es kann gezeigt werden, dass
$$
\sum_{l=0}^n \sum_{m=-l}^l f_l^m \, H_l^m(\theta, \phi) = \sum_{m=-n}^n \sum_{l=-n}^n c_l^m \, e^{i \, k \theta} \, e^{i \, m \phi}
$$
gilt. Das bedeutet, dass im Fall äquidistanter Richtungen die Synthese mithilfe einer 2D-FFT berechnet werden kann.
Plots
Nachfolgend Plots zu den ersten 5 Bändern.
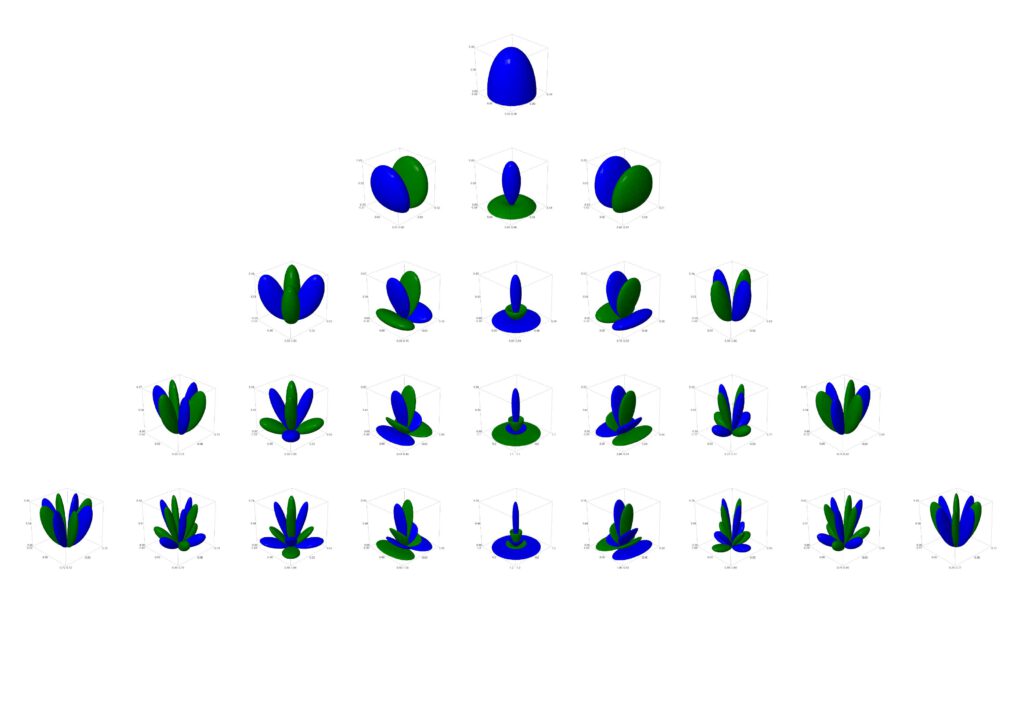
Hier oder unter “Hemispherical Harmonics auf GitHub” ein entsprechendes SageMath-Script zum Plot der Basisfunktionen.
Quellen
- (2004): A Novel Hemispherical Basis for Accurate and Efficient Rendering. In: Keller, Alexander; Jensen, Henrik Wann (Hrsg.): Eurographics Workshop on Rendering, The Eurographics Association, 2004, ISSN: 1727-3463.