Signalverarbeitung ist in vielen Anwendungen zentral. Von der drahtlosen Kommunikation über akustische Messungen bis zur Seismologie müssen große Datenströme in Echtzeit ausgewertet werden. Häufig geht es darum, in verrauschten Signalen bekannte Muster zu erkennen, zum Beispiel den Beginn einer Übertragung oder die Signatur einer Quelle.
Mathematisch basiert diese Mustererkennung auf Korrelationen und Faltungen, die die Ähnlichkeit zweier Signale quantifizieren. Das gilt gleichermaßen für Übertragungssignale (Kommunikation), akustische Messreihen und seismische Daten.
Allen diesen Anwendungen ist gemeinsam, dass sehr große Datenfenster mit immer gleichen Operationen verarbeitet werden. Die Berechnungen sind daher rechenintensiv, profitieren aber stark von Parallelität: Moderne GPUs beschleunigen klassische Verfahren wie FFT-basierte Filter, Kreuzkorrelationen und Decoding deutlich, weil viele identische Operationen gleichzeitig ausgeführt werden. In unseren Experimenten wurde mit Python und einer CUDA-Bibliothek auf Standardhardware bis zu 30-fach schneller gerechnet als gegenüber einer CPU-Single-Thread-Referenz und gegenüber einer 16-Thread-CPU lag die Beschleunigung bei rund 15×.
Im Folgenden wird gezeigt, wie sich diese Berechnung effizient umsetzen lässt. Der Fokus liegt nicht auf der physikalischen Übertragung, sondern auf der mathematischen Struktur der Verfahren und ihrer Implementierung auf der GPU.
Einordnung in den Kontext der kanalnahen Signalverarbeitung (PHY ↔ MAC)
Wir betrachten als zentrales Problem die Präambel-Detektion. Darunter versteht man das Auffinden einer bekannten Bit- oder Samplesequenz am Beginn eines Rahmens in einem verrauschten Eingangssignal. Die Präambel markiert den Start des Datenblocks und ermöglicht eine erste Synchronisation in Zeit und ggf. Frequenz. Technisch entspricht dies einer Mustererkennung über Kreuzkorrelation bzw. einem angepassten Filter.
Die Präambel-Detektion sitzt unmittelbar an der Schnittstelle zwischen Physical Layer (PHY, Layer 1) und Media Access Control (MAC), der unteren Teilschicht des Data-Link-Layers (Layer 2) im OSI-Schichtenmodell. Hier werden kontinuierliche Eingangssignale in strukturierte Datenblöcke überführt, synchronisiert und für die weitere Verarbeitung bereitgestellt. Die MAC-Schicht liegt unmittelbar über Layer 1 und steuert den Zugriff auf das Übertragungsmedium.
In Layer 1 dominieren Algorithmen und Verfahren wie Faltung, FFT und Kreuzkorrelation. Diese sind stark parallelisierbar und damit für GPUs besonders geeignet.
Synchronisation und Weiterverarbeitung
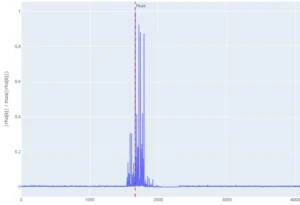
Die Präambel wird durch die Kreuzkorrelation detektiert. Der maximale Korrelationswert kennzeichnet die Peak-Position und damit den Start des Frames. Aus der Phase an dieser Position lässt sich bei komplexen Basisbandsignalen ein grober Frequenzversatz abschätzen. Auf die Grobsynchronisation folgen Feinkorrekturen von Zeit und Frequenz sowie bei Bedarf eine Kanalschätzung mit bekannten Referenz- oder Pilotsymbolen, um die Kanalantwort zu bestimmen, und anschließend die Entzerrung (Equalization) zur Kompensation der Kanalverzerrungen. Das Ergebnis sind zeitlich ausgerichtete und — soweit erforderlich — entzerrte Symbole.
Darauf aufbauend erfolgen Demodulation und Dekodierung. Die Demodulation liefert Zuverlässigkeitswerte für die Bits (LLRs), die — nach Deinterleaving — in der Vorwärtsfehlerkorrektur (FEC) genutzt werden, z. B. LDPC oder Polar. Diese Verfahren beruhen auf linearer Algebra über dem Binärkörper \(\mathbb{F}_2\) und den Vektorräumen \(\mathbb{F}_2^N\) und umfassen Operationen mit Generator- und Paritätsprüfmatrizen sowie Faltungs- und Blockcodes als Matrix- und Vektoroperationen. Die Qualität der Synchronisation wirkt direkt auf die Fehlerquote der Dekodierung.
Matched Filter und effiziente Berechnung der Kreuzkorrelation
Im Rauschfall ist die Kreuzkorrelation dem Matched Filter gleichwertig und damit das geeignete Mittel zur zuverlässigen Präambel-Detektion. Uns interessiert die effiziente Umsetzung: Statt vieler Einzelsummen über alle Verschiebungen berechnen wir die Korrelation per FFT, multiplizieren die Spektren komponentenweise und transformieren zurück. Für die Detektion wird der „valid“-Bereich ausgewertet. Im Beispiel arbeiten wir mit reellen oder komplexen Samples, typisch float32 bzw. complex64.
Kontinuierliche Kreuzkorrelation
Seien \(x,y \in L^2(\mathbb{R})\) (quadratintegrabler, komplexwertiger Funktionen). Die Kreuzkorrelation von \(x\) und \(y\) ist die Funktion \(R_{xy}:\mathbb{R}\to\mathbb{C}\), definiert durch
\[
R_{xy}(\tau) \;:=\; \int_{-\infty}^{\infty} x(t+\tau)\,\overline{y(t)}\,\mathrm{d}t
\;=\; \big\langle x(\cdot+\tau),\,y(\cdot) \big\rangle_{L^2}, \qquad \tau \in \mathbb{R}.
\]
Diskrete Kreuzkorrelation
Seien \(x,y \in \ell^2(\mathbb{Z})\) (quadratsummierbare, komplexwertige Folgen). Die diskrete Kreuzkorrelation von \(x\) und \(y\) ist die Folge \(R_{xy}:\mathbb{Z}\to\mathbb{C}\), definiert durch
\[
R_{xy}[k] \;:=\; \sum_{n\in\mathbb{Z}} x[n+k]\,\overline{y[n]}
\;=\; \big\langle x[\cdot+k],\,y[\cdot] \big\rangle_{\ell^{2}}, \qquad k\in\mathbb{Z}.
\]
Vom kontinuierlichen Modell zum endlichen Vektor
In realen Anwendungen arbeiten wir mit endlichen Ausschnitten des Eingangssignals: Ein Datenfenster der Länge \(N\) (z. B. \(2048\), \(4096\), …) und eine bekannte Präambel der Länge \(M\). Aus den Zeitreihen werden so Vektoren \(x \in \mathbb{C}^{N}\) (Daten) und \(p \in \mathbb{C}^{M}\) (Präambel). Die Kreuzkorrelation wird dann zu einer neuen Folge (bzw. einem Vektor) von Ähnlichkeitswerten entlang verschiedener Verschiebungen („Lags“).
Normierte Kreuzkorrelation
Die normierte Kreuzkorrelation misst die Ähnlichkeit zwischen einem Signalabschnitt und der Vorlage, skaliert auf deren Energien:
\[
\rho_{x p}[k] \;=\; \frac{R_{x p}[k]}{\;\lVert x_k\rVert_{2}\,\lVert p\rVert_{2}\;}
\]
\[
x_k := \big[x[k],\,\dots,\,x[k+M-1]\big]^{\top}, \qquad M=\lvert p\rvert, \qquad k=0,\dots,N-M
\]
Dabei ist \(x_k\) der Länge-\(M\)-Ausschnitt des Datenfensters, beginnend bei Index \(k\) (gleitendes Fenster).
Für reelle Signale gilt \(\rho \in [-1,1]\) (Cosine Similarity). Bei komplexen Signalen gilt \(|\rho|\le 1\); das Argument \(\arg(\rho)\) entspricht dem Phasenversatz. Ein hoher Peak von \(|\rho[k]|\) nahe 1 deutet auf einen sicheren Match hin, die Peak-Position entspricht dem Startindex. Eine Zero-Mean-Variante (Zentrierung vor der Normierung) ist optional und robuster gegenüber DC-Offsets und langsamen Pegeltrends (Drift).
Kreuzkovarianz
Die Kreuzkovarianz (engl. cross-covariance) ergibt sich als Kreuzkorrelation der mittelwertfreien Signale. Für gegebene Signale \(x,y\) über ein Datenfenster der Länge \(N\) seien die Stichprobenmittel
\begin{equation}
\mu_x \;=\; \frac{1}{N}\sum_{n=0}^{N-1} x[n],
\qquad
\mu_y \;=\; \frac{1}{N}\sum_{n=0}^{N-1} y[n].
\label{eq:means}
\end{equation}
Mit den zentrierten Signalen \(\tilde x[n]=x[n]-\mu_x\) und \( \tilde y[n]=y[n]-\mu_y\) ist die Kreuzkovarianz definiert als
\begin{equation}
C_{xy}[k] \;=\; \sum_{n} \bigl(x[n+k]-\mu_x\bigr)\,
\overline{\bigl(y[n]-\mu_y\bigr)}.
\label{eq:xcov-def}
\end{equation}
D. h. es gilt
\begin{equation}
C_{xy}[k] \;=\; R_{\tilde x\,\tilde y}[k]
\;=\; R_{\,x-\mu_x,\;y-\mu_y}[k].
\label{eq:xcov-as-xcorr}
\end{equation}
Warum das schnell sein muss
Für jede Verschiebung \(k\) wird eine Summe über die \(M\) überlappenden Samples aus \(x\) und \(p\) gebildet. Beim „valid“-Ausschnitt gibt es \(\#k = N – M + 1\) zulässige Verschiebungen, denn das \(M\)-lange Fenster \(x_k\) muss vollständig im Datenfenster liegen. Der naive Aufwand beträgt damit etwa \(M \cdot (N – M + 1)\), also \(\mathcal{O}(N \cdot M)\). In vielen Anwendungen ist \(M \ll N\); dann wächst der Aufwand im Wesentlichen linear mit \(N\), jedoch mit dem Faktor \(M\). Bei großen Fenstern, vielen Kanälen oder mehreren Vorlagen summiert sich das schnell zu hohen Laufzeiten.
Die schnelle Lösung: FFT-Korrelation
Statt jede Verschiebung einzeln zu berechnen,
\[
R^{\mathrm{valid}}_{x p}
\;=\;
\Big(\; \sum_{n=0}^{M-1} x[n+k]\;\overline{p[n]} \;\Big)_{\,k=0}^{\,N-M}
\;\in\; \mathbb{C}^{\,N-M+1}
\]
nutzen wir die Schnelle Fourier-Transformation (FFT) und das Korrelations-/Faltungstheorem einmal in den Frequenzbereich transformieren, dort komponentenweise multiplizieren, anschließend zurücktransformieren.
\[
R_{x p} \;=\; \mathcal{F}^{-1}\!\left\{\,\mathcal{F}\{x\}\cdot \overline{\mathcal{F}\{p\}}\,\right\}.
\]
Damit sinkt die Komplexität von \(\mathcal{O}(N M)\) auf zwei Vorwärts-FFTs, ein Hadamard-Produkt und eine inverse FFT. Um lineare statt zirkulärer Korrelation zu erhalten, arbeiten wir mit Zero Padding auf eine Länge \(L \ge N + M – 1\). Das Ergebnis hat Länge \(N+M-1\) und genutzt wird der „valid“-Bereich \(k=0,\dots,N-M\). Insgesamt liegt der Aufwand in der Größenordnung \(\mathcal{O}(L \log L)\).
In der Implementierung verwenden wir die diskrete Form des Theorems mit einer DFT der Länge \(L\)
\[
R_{x p}^{(\mathrm{lin})}
\;=\;
\mathcal{F}_L^{-1}\!\left\{\,\mathcal{F}_L\{x_{\mathrm{zp}}\}\cdot \overline{\mathcal{F}_L\{p_{\mathrm{zp}}\}}\,\right\},
\qquad L \ge N + M – 1 .
\]
\(\mathcal{F}_L\) bezeichnet die DFT der Länge \(L\). Die Berechnung erfolgt vollständig im Frequenzraum mit GPU-FFT-Bibliotheken und ausgelesen wird anschließend der „valid“-Ausschnitt.
Ablauf in der Praxis
Vorbereitung der FFT-Pipeline
-
Daten in den VRAM bringen.
Eingang \(x\in\mathbb{C}^N\) (Fenster) und Präambel \(p\in\mathbb{C}^M\) als GPU-Array anlegen, meist incomplex64. Kommen die Daten vom Host, sorgen pinned memory und asynchrone Kopien dafür, dass Übertragung und Berechnung überlappen können [1]. -
FFT-Länge wählen und vorallozieren.
Zero Padding auf \(L \ge N+M-1\) wählen, häufig die nächstgrößere Zweierpotenz. Puffer für Spektren und Ergebnis einmalig in Größe \(L\) allozieren und für nachfolgende Fenster wiederverwenden, um Allokations-Overhead zu vermeiden. -
Referenzspektrum vorbereiten.
\(P=\mathcal{F}\{p_{\mathrm{zp}}\}\) einmal berechnen und die konjugierte Version \(\overline{P}\) ablegen. Bei mehreren Präambeln empfiehlt sich ein kleiner Zwischenspeicher, etwa ein Dictionary nach \(M\) und \(L\), um die Wiederverwendung zu steuern.
Lauf für jedes Eingangsfenster
Es wird jeweils ein Fenster der Länge \(N\) verarbeitet. Bei Streams können die Fenster nacheinander (mit oder ohne Überlappung) oder in Batches laufen.
-
FFT-Korrelation pro Datenfenster (Länge N).
Vorwärts in den Frequenzbereich transformieren, die Spektren komponentenweise multiplizieren und danach zurücktransformieren. So entsteht das Korrelationssignal der Länge L, aus dem der nutzbare Bereich für die Detektion entnommen wird.# F steht stellvertretend für die FFT-Funktionen deiner Bibliothek # (z. B. cuFFT, CuPy, PyTorch, oneMKL, FFTW) # Gegeben: x (len N), p (len M), L >= N + M - 1 X = F.fft(x, L) P = F.fft(p, L) # Frequenzbereich: Korrelationsprodukt und inverse FFT R_full = F.ifft(X * F.conj(P)) # Länge L -
valid-Ausschnitt des Datenfensters bilden.
Weiterverarbeitet wird der mittlere Abschnitt, in dem die Präambel das Fenster vollständig überdeckt. Nur dort sind die Korrelationswerte aussagekräftig und dienen als Basis für die Peak-Suche. -
Normierung.
Zur Kompensation von Pegelschwankungen die normierte Kreuzkorrelation \(\rho[k]\) verwenden. Die lokalen Energien als Gleitfenster-Summen bestimmen oder als Faltung mit einem Eins-Fenster der Länge \(M\). -
Peak bestimmen.
Nimm den größten Wert als Start und ignoriere kleine Treffer. -
Transfers minimieren und parallelisieren.
Nur die wirklich benötigten Ergebnisse auf den Host zurückgeben, zum Beispiel Peak-Index und Wert. Mehrere Fenster als Batch an die FFT-Bibliothek übergeben, um die GPU auszulasten, und Kopien sowie Berechnung so planen, dass keine Leerlaufzeiten entstehen.
- (1) Große Arrays bleiben bis zur Peak-Erkennung im VRAM. Nur finale Ergebnisse oder Indizes werden kopiert.
- (2) Die FFT von \(p\) für gegebenes \(L\) einmalig vorab berechnen und wiederverwenden.
- (3) Für Streams und Batching mehrere Fenster parallel mit der GPU-FFT verarbeiten.
Verwendete Bibliotheken
-
CuPy – Python-Array-API auf der GPU (
cp.ndarray,cp.fft), weitgehend kompatibel zu NumPy (Website). -
cuFFT – NVIDIA-FFT-Bibliothek, von
cp.fft.fft/cp.fft.ifftgenutzt (Info). - PyFFTW – schneller FFT-Wrapper für die CPU auf Basis von FFTW, mit Mehrthreading-Unterstützung (Doku, FFTW).
-
NumPy (Fallback) – identische API auf der CPU (
numpy.ndarray,np.fft) für Systeme ohne GPU (Website).
Alternativen je nach Hardware: PyTorch-FFT auf ROCm, SYCL/oneMKL DFT, FFTW direkt auf der CPU.
Optional: kompakter CuPy-Code (alles im VRAM)
import cupy as cp
# Eingaben
x = cp.asarray(signal, dtype=cp.complex64) # Länge N
p = cp.asarray(template, dtype=cp.complex64) # Länge M
N, M = x.size, p.size
# FFT-Länge L >= N+M-1 (nächste Zweierpotenz)
L = 1 << (N + M - 2).bit_length()
# Zero-Padding + FFTs
X = cp.fft.fft(x, L)
P = cp.fft.fft(p, L)
# Frequenzbereich: Korrelationsprodukt und inverse FFT
R_full = cp.fft.ifft(X * cp.conj(P)) # lineare Anteile: R_full[:N+M-1]
# valid-Ausschnitt (k = 0 .. N-M)
start = M - 1
stop = start + (N - M + 1)
R_valid = R_full[start:stop]
# Optionale Normierung (pegelrobust)
E_p = cp.sum(cp.abs(p)**2)
win = cp.ones(M, dtype=cp.float32)
E_x = cp.convolve(cp.abs(x)**2, win, mode="valid") # Länge N-M+1
rho = R_valid / cp.sqrt(cp.maximum(E_x * E_p, 1e-9))
Numerische Auswertung
Für die Leistungsbewertung wurden zwei CPU-Szenarien getestet – Single-Thread und 16 Threads – und mit der GPU-Implementierung der Kreuzkorrelation verglichen. Gemessen wurde auf folgender Hardware:
- CPU: AMD Ryzen 9 5950X (16 cores)
- GPU: NVIDIA GeForce RTX 3080
Die Laufzeiten beziehen sich auf Blockgrößen zwischen 8 k und 16 M Samples und umfassen die komplette Pipeline von der Vorbereitung bis zur Peak-Bestimmung.
| Ntotal (Samples) | Profil | GPU ttot [ms] | CPU 16 Threads [ms] | CPU 1 Thread [ms] | Speedup vs 16T | Speedup vs 1T |
|---|---|---|---|---|---|---|
| 8 192 | demo_small | 2.53 | 48.56 | 47.47 | 19× | 19× |
| 262 144 | demo_medium | 5.49 | 20.56 | 34.27 | 4× | 6× |
| 1 048 576 | demo_large | 8.76 | 92.97 | 154.52 | 11× | 18× |
| 4 194 304 | demo_xl | 24.12 | 372.23 | 736.36 | 15× | 31× |
| 16 777 216 | demo_xxl | 90.36 | 1 285.09 | 2 997.96 | 14× | 33× |
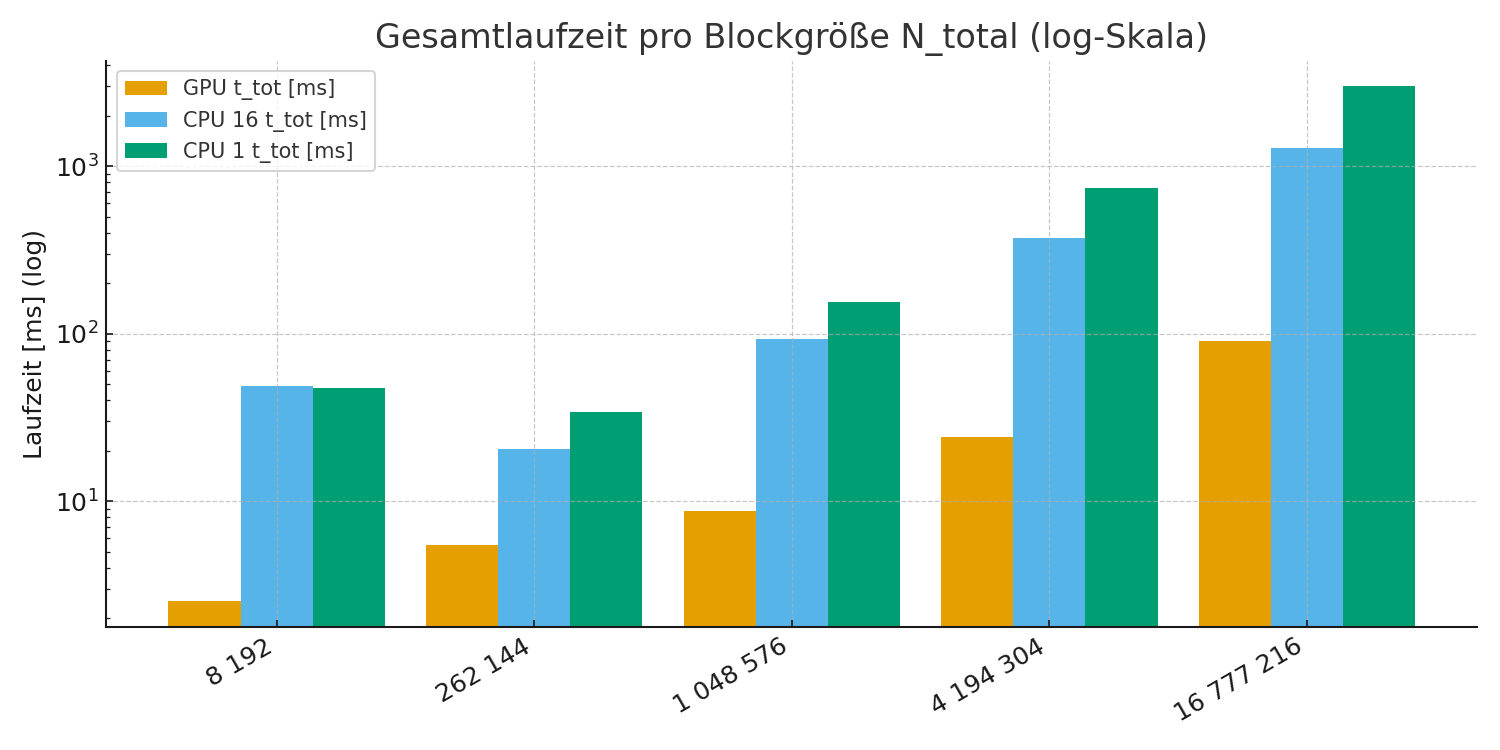
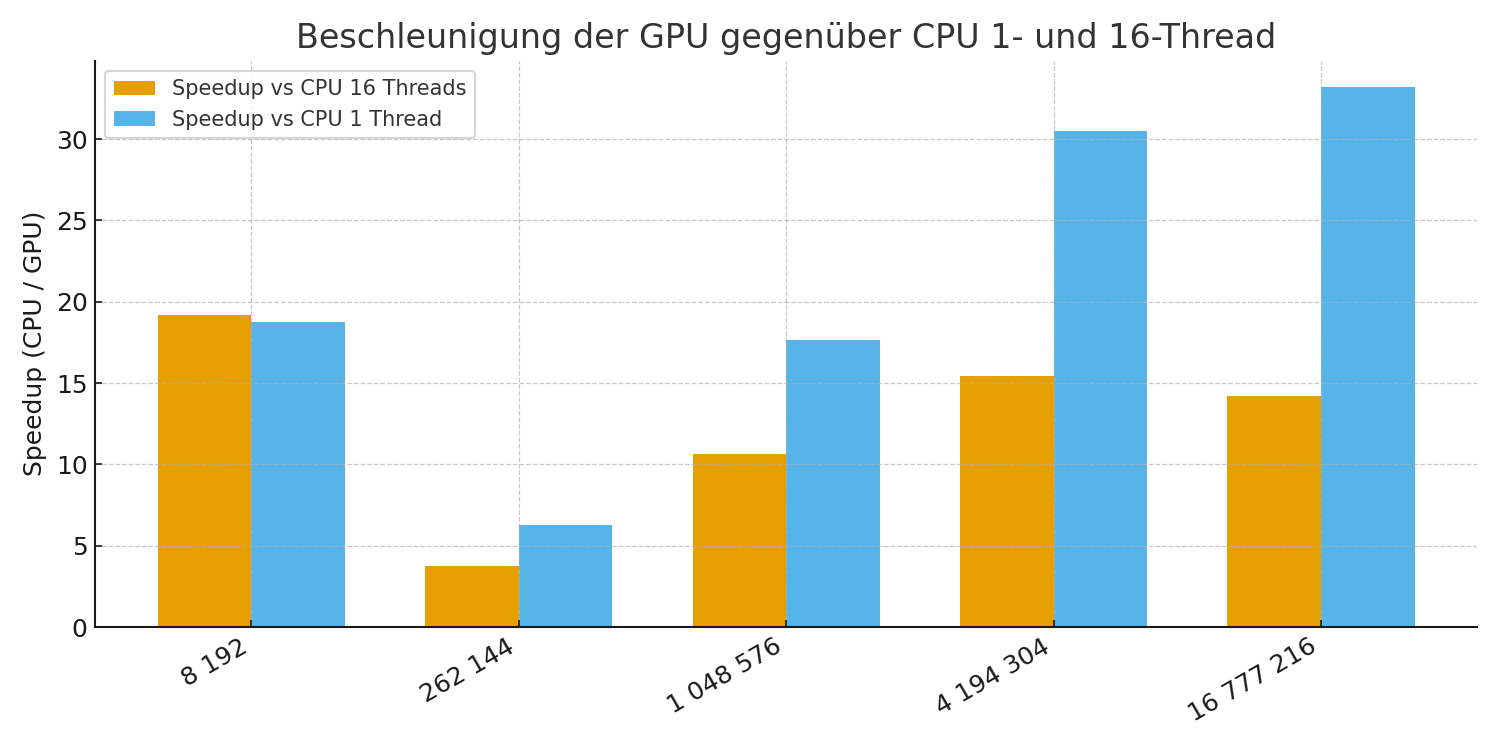
Die GPU reduziert die Laufzeit deutlich. Gegenüber der 16-Thread-Variante liegt der maximale Speedup bei rund 19×, gegenüber einer Single-Core-Ausführung bei über 30×. Für kleine Blockgrößen dominieren Start-Overheads, ab mittleren Größen spielt die GPU ihre Parallelität voll aus.
Gesamtlaufzeiten auf logarithmischer Skala
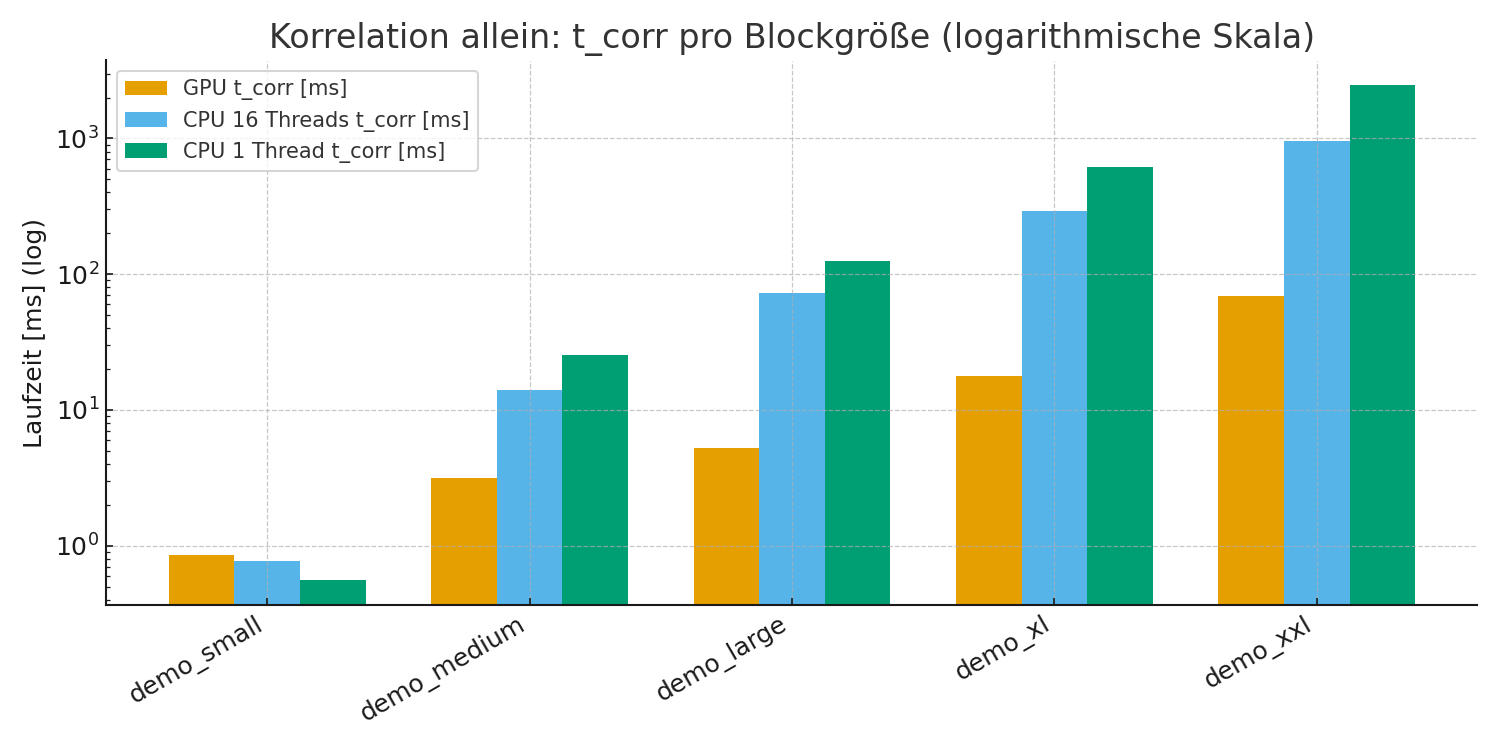
Korrelation allein auf logarithmischer Skala
Speedup der GPU
Beobachtungen
- FFT-Pfad (PyFFTW): Durch Umstellung von 1 auf 16 Threads sinkt die CPU-Zeit im XXL-Szenario von ca. 4.4 s (NumPy, single thread) auf rund 0.95 s (PyFFTW, 16 Threads). Die GPU liegt mit ca. 70 ms weiterhin deutlich vorn.
- Skalierung: Bei sehr kleinen Blöcken dominieren Start-Overheads, weshalb ein CPU-Fallback sinnvoll sein kann. Ab mittleren Blockgrößen spielt die GPU ihre Stärken bei Durchsatz und Latenz aus. Zwischen 1 und 16 Threads zeigt die CPU nahezu lineare Skalierung, erreicht aber nicht das Niveau der GPU.
Fazit und Ausblick
Die Ergebnisse stammen aus einem ersten ad-hoc Test und dienen als Orientierung. Weitere Optimierungen und modernere Hardware versprechen bessere Resultate.
Die GPU reduziert die Laufzeit der Kreuzkorrelation von mehreren hundert Millisekunden auf wenige Millisekunden. Auf unserem Testsystem wurde ein Speedup von bis zu 30× gegenüber Single-Thread und bis zu ~19× gegenüber 16 Threads erreicht. Ähnliche Beschleunigungen sind auch für weitere Algorithmen und Verfahren zu erwarten, etwa für FEC/LDPC, die stark von paralleler linearer Algebra profitieren.
Als nächste Schritte bietet sich eine Umsetzung in C++ mit CUDA oder SYCL an, was Performance und Portabilität erhöht und die Nutzung passender FFT-Backends wie oneMKL oder plattformspezifischer DFT-Routinen ermöglicht. Die Pipelines lassen sich weiter beschleunigen durch batched Ausführung, rFFT/irFFT bei reellen Daten und die konsequente Wiederverwendung vorberechneter Spektren. Ein gezieltes Profiling hilft Engpässe früh zu erkennen. Unter NVIDIA stehen Nsight Tools zur Verfügung, vergleichbare Werkzeuge sind ROCTx und rocprof bei AMD sowie VTune bei Intel. Perspektivisch interessant: SYCL verspricht neben CPU und GPU auch die Ausführung auf FPGAs, was sich als eigenes Projekt-Thema anbietet.
[1] Kurze Erläuterung zu Host↔Device-Transfers, pinned memory und CUDA-Streams folgt in einem eigenen Beitrag