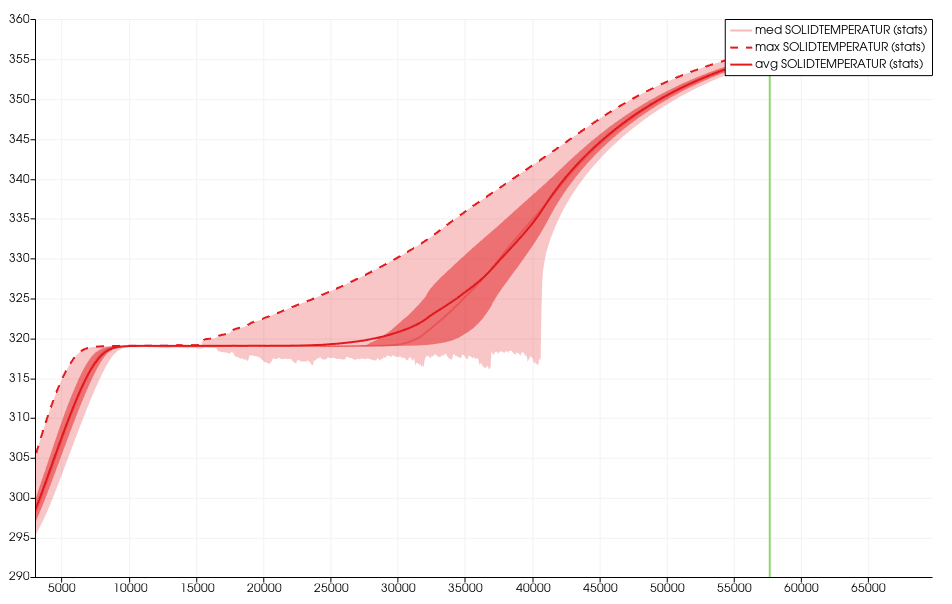
In diesem Beitrag zeige ich eine Visualisierung des Phasenwechsels eines Paraffin-Blocks, der als PCM (Phase Change Material) dient. Die Simulation basiert auf der Enthalpie-Gleichung, die den Wärmeübergang mit Phasenwechsel beschreibt.
Die numerischen Ergebnisse wurden mit ParaView ausgewertet und als Video zusammengestellt. Der Film zeigt das sukzessive Aufschmelzen des Materials: vom festen Zustand über eine mushy zone (teilweise geschmolzen) bis zur vollständig flüssigen Phase.
Das zugrundeliegende physikalische Modell eignet sich für die Beschreibung latenter Wärmespeicher. Es wird in vielen Bereichen eingesetzt – etwa in der Bauphysik, der Fahrzeugklimatisierung, der Energietechnik sowie im geothermischen Bereich.
Enthalpie-Gleichung (Phasenwechsel)
Zur Beschreibung von Schmelz- und Erstarrungsvorgängen verwenden wir die Enthalpieformulierung. Dabei bezeichnet \(E(x,t)\) die Volumen-Enthalpie (Energie pro Volumen) und \(T(x,t)\) die Temperatur. Mit Fourier-Wärmeleitung und einer effektiven Wärmeleitfähigkeit \(\lambda\) ergibt sich
die Energiebilanz
\[
E_t \;-\; \nabla\!\cdot\!\bigl(\lambda\,\nabla T(E)\bigr) \;=\; f,
\]
wobei \(f\) Volumenquellen bzw. -senken (W m\(^{-3}\)) umfasst. Die Kopplung erfolgt über die materiale Beziehung \(T=T(E)\): Aus der lokal gespeicherten Energie \(E\) wird die Temperatur bestimmt. Dies ist der wesentliche Vorteil der Enthalpieform: die latente Wärme ist in \(E\) bereits enthalten.
Physikalischer Kern: latente Wärme
Im Schmelzbereich bleibt die Temperatur trotz Energiezufuhr unverändert: Die zugeführte Energie wird zum Phasenübergang benötigt (latente Wärme). Mathematisch entspricht das einem isothermen Abschnitt in der Funktion \(T(E)\) — die Temperatur „steht“ bei \(T_m\), bis die gesamte Schmelzenthalpie aufgenommen wurde.
Stückweise Beziehung \(T(E)\)
\[
T(E) \;=\;
\begin{cases}
T_m + \dfrac{E}{\rho_S\,c_S}, & \text{für } E \le 0 \quad (\text{fest}),\\[8pt]
T_m, & \text{für } E \in (0,\,\rho_L L) \quad (\text{mushy/interface}),\\[8pt]
T_m + \dfrac{E-\rho_L L}{\rho_L\,c_L}, & \text{für } E \ge \rho_L L \quad (\text{flüssig}).
\end{cases}
\]
Hierbei sind \(\rho_S, \rho_L\) die Dichten und \(c_S, c_L\) die (hier als konstant angenommenen) Wärmekapazitäten in der festen bzw. flüssigen Phase; \(L\) ist die spezifische Schmelzenthalpie und \(T_m\) die Schmelztemperatur. Der Bereich \((0,\rho_L L)\) bildet die sogenannte mushy zone, in der der Phasenanteil zwischen fest und flüssig übergeht und \(T\) isotherm bleibt.
Inverse Beziehung \(E(T)\)
Für Auswertungen ist zusätzlich die inverse Abbildung nützlich; bei konstanten Materialwerten innerhalb einer Phase gilt
\[
E(T) \;=\;
\begin{cases}
\rho_S\,c_S\,(T – T_m), & \text{für } T < T_m,\\[6pt]
(0,\,\rho_L L), & \text{für } T = T_m,\\[6pt]
\rho_L\,c_L\,(T - T_m) + \rho_L L, & \text{für } T > T_m.
\end{cases}
\]
Die mittlere Zeile signalisiert, dass im isothermen Schmelzfall der Enthalpiezustand irgendeinen Wert zwischen \(0\) und \(\rho_L L\) annehmen kann (abhängig vom lokalen Phasenanteil), ohne dass sich \(T\) ändert.
Semi-diskreter Ansatz
Ausgehend von \(\;E_t – \nabla\!\cdot(\lambda\nabla T(E)) = f\;\) ersetzen wir die Zeitableitung durch den Differenzenquotienten \(\;E_t \approx \dfrac{E^{k+1}-E^{k}}{\Delta t}\;\) und diskretisieren den Raum (FEM/FVM) mit Massenmatrix \(M_h\) und Steifigkeitsmatrix \(S_h\). Das ergibt
\[
\frac{1}{\Delta t}\,M_h\!\left(E_h^{\,k+1}-E_h^{\,k}\right)
\;+\; S_h\,T_h^{\,k+1}
\;=\; f_h^{\,k+1}.
\]
Durch Umformen erhalten wir die kompakte Schreibweise
\[
M_h\,E_h^{\,k+1} \;+\; \Delta t\,S_h\,T_h^{\,k+1} \;=\; f_h^{\,k+1},
\qquad
T_h^{\,k+1} \;=\; T\!\bigl(E_h^{\,k+1}\bigr).
\]
Die rechte Seite \(f_h^{\,k+1}\) enthält u. a. den Term \(M_h\,E_h^{\,k}\) sowie die Beiträge aus den (Orts-)Randbedingungen. Bei Robin-Randbedingungen (Wärmeübergang) gehen entsprechende Anteile zusätzlich in die Steifigkeitsmatrix \(S_h\) ein.
Nichtlinearität und Newton-Verfahren
Das Gleichungssystem ist nichtlinear, weil die Temperatur über \(T=T(E)\) und optional temperaturabhängige Größen wie \(\lambda(T)\) oder \(c(T)\) von der gesuchten Enthalpie abhängen. Pro Zeitschritt nutzen wir daher ein Newton-Verfahren. Typischer Startwert ist der Enthalpiezustand des vorherigen Schritts. In jeder Newton-Iteration werden zunächst aus der aktuellen Enthalpie Temperatur und Materialgesetz berechnet, anschließend Residuum und Jacobi-Matrix konsistent neu assembliert und danach das lineare Korrektursystem gelöst. Die Enthalpie wird mit dem gefundenen Korrekturschritt aktualisiert. Weil \(T\) direkt von \(E\) abhängt, ändern sich die Ableitungen und damit die Jacobi-Matrix in jedem Schritt, sodass sie innerhalb der Newton-Schleife immer wieder aufgebaut wird. Eine Dämpfung oder Line-Search erhöht die Robustheit, besonders in der Nähe der Phasenwechselzone. Abbruch erfolgt, wenn Änderungen oder Residuen unter vordefinierte Toleranzen fallen. Bei Konvergenzproblemen helfen kleinere Zeitschritte, eine Regularisierung der mushy zone oder ein besserer Vorkonditionierer.
Testbeispiel
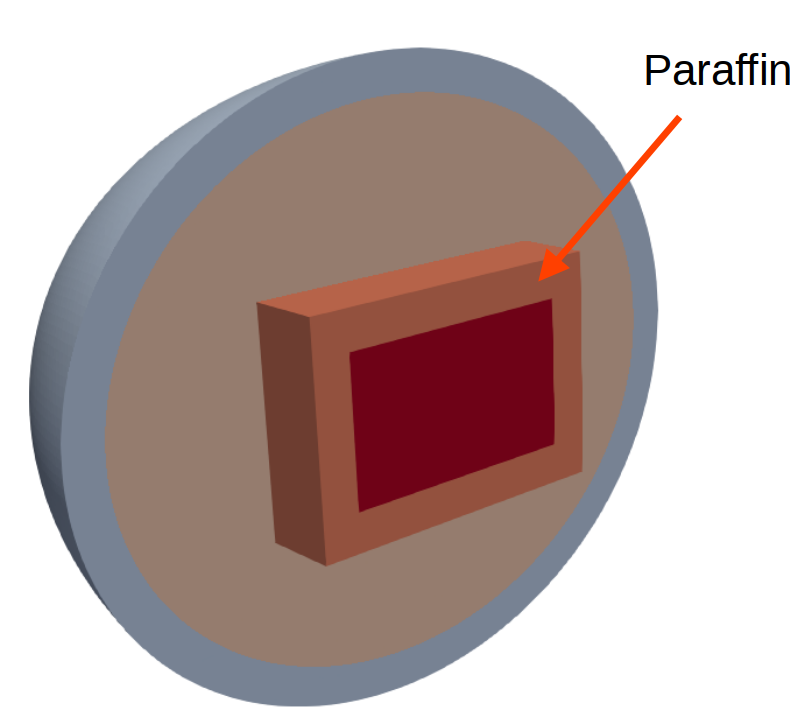
Die folgenden beiden Videos zeigen den zeitlichen Verlauf des Phasenwechsels in einem Paraffin-Block (Phase Change Material, PCM), der als thermischer Schutz für eine innenliegende Elektronik dient. Die Simulation basiert auf der Enthalpie-Gleichung, welche sowohl die Temperaturentwicklung als auch die beim Phasenwechsel auftretenden Phänomene (latente Wärme) erfasst.
- Video 1 (Abb. 1): Entstehung und Ausbreitung der mushy zone – also des teils geschmolzenen Bereichs – sowie der anschließende Übergang in die vollständig flüssige Phase.
- Video 2 (Abb. 2): Visualisierung der verbleibenden festen Phase des Paraffins. Diese nimmt im Zeitverlauf stetig ab, bis sie vollständig abgeschmolzen ist.
Durch den Phasenwechsel von fest zu flüssig wird ein großer Teil der eingetragenen Wärmeenergie im Material gespeichert, ohne dass die Temperatur ansteigt. Diese sogenannte latente Wärme bewirkt eine deutliche Verzögerung der Temperaturerhöhung im inneren Bereich. Der Paraffin-Block fungiert somit als thermischer Puffer und schützt die empfindliche Elektronik wirksam vor Überhitzung.
