In diesem Beitrag geht es um die automatische Anomalieerkennung in Zeitreihen. Ziel ist die automatische Erkennung von Abweichungen vom Normalbetrieb. Das Ergebnis ist ein kontinuierlicher Anomaliescore, der sich direkt für Warn- und Alarmstufen nutzen lässt. Inhaltlich knüpft der Beitrag an Anomalieerkennung in Zeitreihen (Teil 1) an. Dort stellte der Beitrag einen Ansatz mit robusten Features und einem Residualscore zur Erkennung auffälligen Verhaltens vor. Der zweite Teil ersetzt diese Featureebene durch ein neuronales Modell, während die Bewertung weiterhin über einen Residualscore läuft.
Der Ansatz ist score-basiert und liefert keine harte Ja-oder-Nein-Entscheidung. Stattdessen verdichtet ein CNN-Encoder jedes hochfrequente Rohsignalfenster zu einem kompakten Vektor im Merkmalsraum (latent space). Darauf arbeitet ein Sequenzmodell (TCN oder GRU), das aus den bisherigen Vektoren den folgenden Vektor prognostiziert. Die Abweichung zwischen Vorhersage und Beobachtung, der Residualscore, ist das zentrale Anomaliesignal.
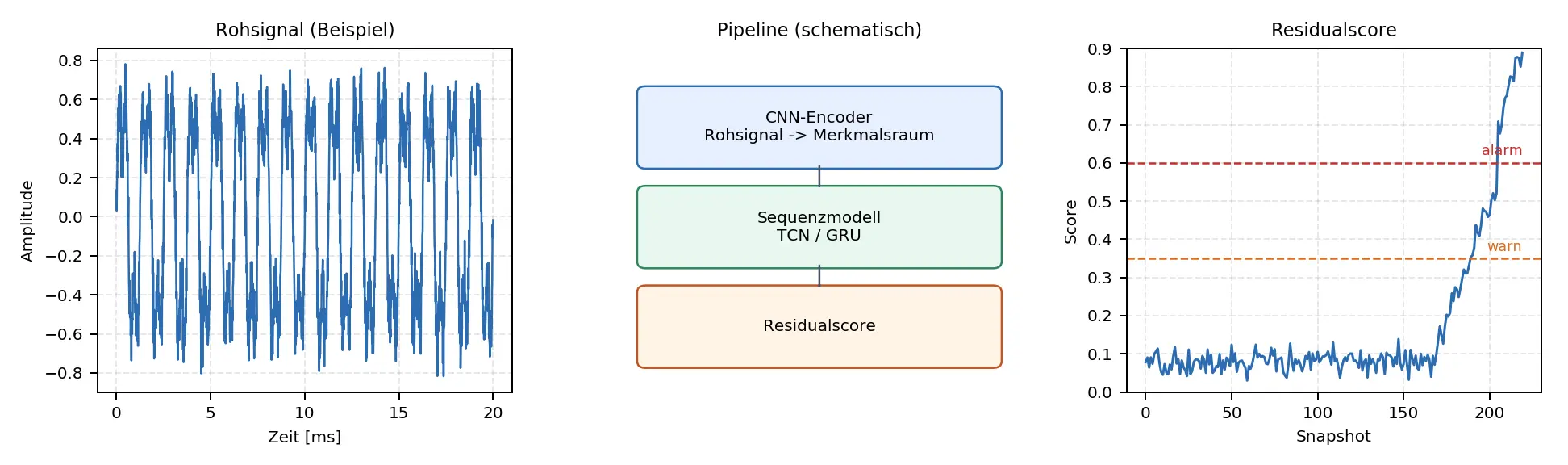
Als Datengrundlage dienen 2156 Dateien (Snapshots) aus dem IMS Bearings Dataset (NASA), Set 1. Jeder Snapshot umfasst einen 1 s Ausschnitt mit 20480 Messwerten pro Kanal und insgesamt liegen 8 Kanäle vor. Die Aufnahmen entstanden im Abstand von 5 beziehungsweise 10 Minuten. Insgesamt ergeben sich 353.239.040 Amplitudenwerte (2156 × 20480 × 8). Pro Kanal entspricht das 44.154.880 Samples und im gezeigten Beispiel werten wir zwei Kanäle aus.
Warum Deep Learning in der Anomalieerkennung?
Deep Learning Modelle sind nicht automatisch besser. Sie werden vor allem dann interessant, wenn Muster komplexer sind als das, was ein lineares Modell stabil abbildet. Typische Fälle sind nichtlineare Dynamik, kombinierte Effekte, mehrere Kanäle oder sehr hochfrequente Rohsignale.
- Vorteil: Das Modell lernt die Merkmalsrepräsentation und benötigt oft weniger Feature Engineering.
- Vorteil: Das Modell erfasst nichtlineare Abweichungen tendenziell besser.
- Nachteil: Der Rechenaufwand ist höher und es gibt mehr Hyperparameter.
- Nachteil: Man muss die Erklärbarkeit aktiv gestalten, zum Beispiel über Score, Kalibrierung und Baselines.
Modellidee: CNN-Encoder und Forecast im Merkmalsraum
Die Pipeline ist modular aufgebaut. Der zentrale Schritt ist der Übergang in einen kompakten Merkmalsraum. Ein CNN-Encoder fasst jedes Rohsignalfenster, zum Beispiel 1 s bei 20 kHz, zu einem Vektor mit \(d\) Dimensionen zusammen. Dieser Vektor ist deutlich kleiner als das Originalsignal und enthält dennoch die für den Zustand relevanten Muster.
Encoder-Details und Merkmalsraum
Mathematisches Detail: Was macht der CNN-Encoder?
Ein Rohsnapshot sei \(x_t\in\mathbb{R}^{C\times N}\) (Kanäle \(C\), Samples \(N\), z. B. \(N=20480\)). Der Encoder ist eine Funktion \(E_\theta\), die das hochdimensionale Rohsignal in einen kompakten Zustandsvektor (latent) abbildet:
\[
z_t = E_\theta(x_t)\in\mathbb{R}^{d},\qquad d\ll C\cdot N.
\]
In der Praxis ist \(E_\theta\) häufig ein 1D-CNN mit Strides (Downsampling) und nichtlinearer Aktivierung. Eine typische Convolution-Schicht (vereinfacht) lässt sich als
\[
h^{(\ell)}_{k,n}=\phi\!\left(\sum_{c=1}^{C_{\ell-1}}\sum_{m=0}^{M-1} w^{(\ell)}_{k,c,m}\,h^{(\ell-1)}_{c,n\cdot s+m}+b^{(\ell)}_{k}\right)
\]
schreiben, mit Filterlänge \(M\), Kanälen \(k\), Aktivierung \(\phi\) (z. B. ReLU) und Stride \(s\), der die Zeitachse komprimiert. Am Ende aggregiert man typischerweise über die Zeit (z. B. Global Average Pooling), um einen festen Vektor \(z_t\) zu erhalten.
Interpretation: Der Encoder lernt automatisch eine Merkmalsrepräsentation, die Impulsfolgen, lokale Muster und bandartige Strukturen im Rohsignal erfasst – also genau das, was man in Teil 1 mit festen Features (RMS, Kurtosis, Bandpower, …) explizit definiert hat.
In Teil 1 kamen einfache, robuste Features zum Einsatz, zum Beispiel Peak to Peak, RMS, Crest Factor, Kurtosis und Bandpower. Diese Größen sind gut interpretierbar und liefern oft schon eine brauchbare Baseline, d. h. einen einfachen Referenzansatz, der als Ausgangspunkt dient und spätere Modelle vergleichbar macht. Im Deep Learning Ansatz legt man diese Features nicht manuell fest, sondern der CNN-Encoder lernt sie direkt aus den Rohdaten. Dadurch kann das Modell auch Kombinationen und Signalanteile nutzen, die in festen Features möglicherweise nicht explizit enthalten sind.
Der CNN-Encoder ist dabei mehr als eine reine Kompression. Er kann hochfrequente Strukturen wie Impulsfolgen oder lokale Muster extrahieren, die ein lineares Modell oder ein festes Feature Set nicht immer sauber abbildet. Damit nutzt das Modell eine Repräsentation, die für die Zustandsänderungen des Systems empfindlich ist, aber gegenüber irrelevanten Signalanteilen robuster bleibt.
Forecast und Residualscore
Ein Forecast Modell arbeitet in diesem Merkmalsraum typischerweise stabiler als direkt auf den Rohpunkten. Statt 20480 Messwerten pro Snapshot verarbeitet das Modell zum Beispiel einen Vektor mit 64 Freiheitsgraden. Dadurch reduziert es den Einfluss von Rauschen, vereinheitlicht die Darstellung und erleichtert die Kalibrierung eines Residualscores.
Die Verarbeitung läuft dann in drei Schritten:
- Aus jedem Rohsnapshot erzeugt der CNN-Encoder einen Merkmalvektor.
- Ein Sequenzmodell, zum Beispiel TCN oder GRU, nutzt eine Folge solcher Vektoren und prognostiziert den nächsten Merkmalsvektor.
- Der Residualscore ist der Abstand zwischen Prognose und Beobachtung im Merkmalsraum und dient als Anomaliescore.
Im Normalbetrieb sagt das Sequenzmodell den nächsten Zustand im Merkmalsraum gut voraus, der Residualscore bleibt klein. Wenn sich das Systemverhalten verändert, zum Beispiel durch Drift oder einen entstehenden Defekt, passt die Vorhersage nicht mehr. Der Abstand zwischen vorhergesagtem und tatsächlichem Merkmalsvektor wächst und der Score steigt.
Trainingsziel und Leakageregel
Wir trainieren ausschließlich auf einer Referenzphase im Normalbetrieb. Zudem leiten wir Schwellenwerte und Normalisierung nur aus dieser Referenzphase ab. Den restlichen Verlauf scoren wir erst danach, damit keine Data Leakage entsteht, denn Testdaten dürfen weder im Training noch in der Kalibrierung enthalten sein. Zur Illustration folgt ein vereinfachter Codeausschnitt:
# --- Training ---
model = RawForecastResidualModel(in_ch=X_raw.shape[1], cfg=cfg).to(device)
opt = torch.optim.AdamW(model.parameters(), lr=1e-3, weight_decay=1e-4)
epoch_max = int(cfg["training"].get("epoch_max", 10))
loss_eps = float(cfg["training"].get("loss_eps", 1e-4))
for epoch in range(1, epoch_max + 1):
loss = train_one_epoch(model, train_loader, opt, device=device)
print(f"epoch {epoch:02d} loss={loss:.6f}")
if loss < loss_eps:
print("early stop")
break
Scoredefinition, Normalisierung und Schwellenwertsetzung sind klar getrennte Schritte.
# --- Evaluation ---
scores = compute_latent_residual_scores(model, dataset, device=device)
# robuste Normalisierung über Referenzphase:
scores_ref = scores[:n_train]
med = np.median(scores_ref)
mad = np.median(np.abs(scores_ref - med)) + 1e-12
score_robust = np.abs(scores - med) / mad
# Schwelle als Quantil der Referenzphase:
q = 0.995
thr = np.quantile(score_robust[:n_train], q)
is_anom = score_robust > thr
Beispiel: IMS Bearing Dataset (Deep-Learning-Variante)
Der Datensatz ist identisch zu Teil 1 (NASA/IMS, Set 1, Bearing 3).
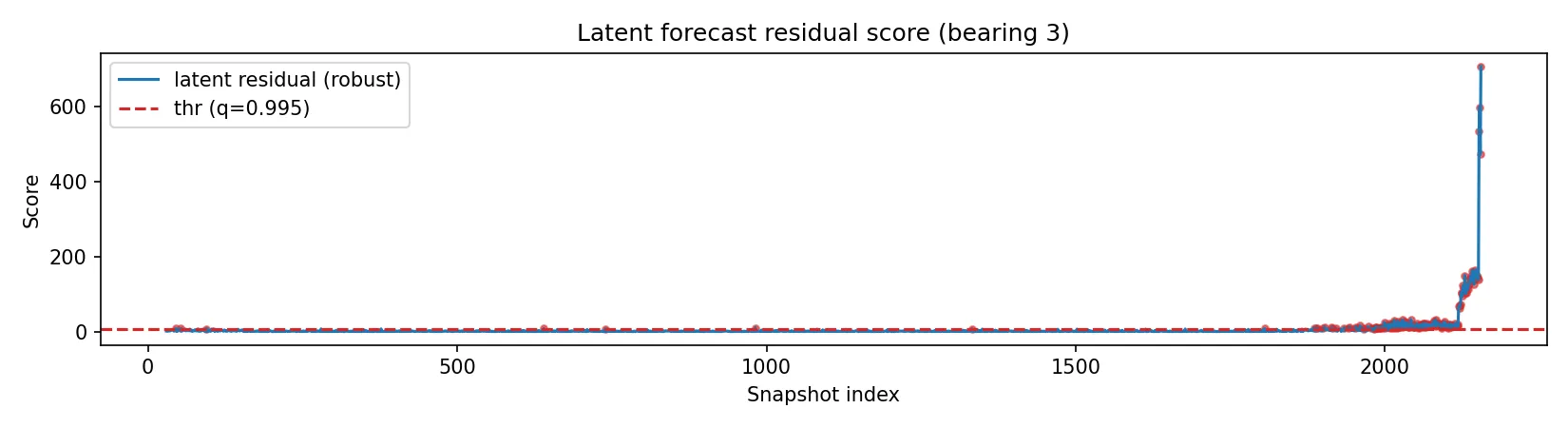
Alarmstufen: Warn und Alarm
Auch hier kalibrieren wir die Schwellenwerte über die Referenzphase, zum Beispiel über Quantile. Zusätzlich lässt sich eine Warnstufe definieren, etwa bei 98,5 Prozent, während die Alarmstufe bei 99,5 Prozent liegt. In der Grafik maskieren wir Überschreitungen innerhalb der Trainingsphase für die Darstellung. Dadurch erkennt man klar, ab welchem Zeitpunkt der Score erstmals außerhalb des Normalbetriebs liegt.

TCN oder GRU: was ist sinnvoller?
Beide Sequenzmodelle sind praxistauglich und eignen sich für Forecastaufgaben im Merkmalsraum.
- TCN (Temporal Convolutional Network) ist effizient, gut skalierbar und in vielen Settings sehr stabil.
- GRU (Gated Recurrent Unit) ist flexibel, kann längere Abhängigkeiten modellieren und reagiert oft empfindlicher auf Hyperparameter.
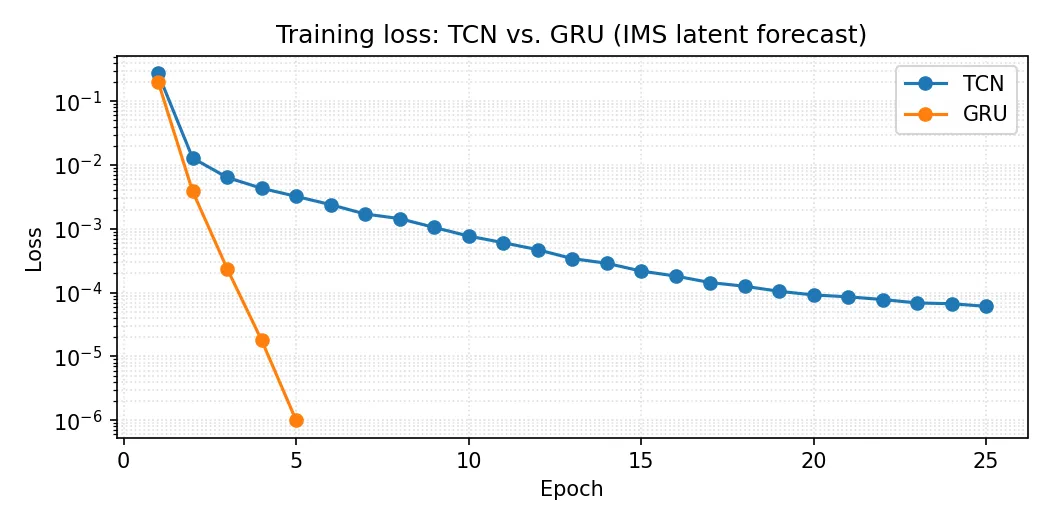
In der IMS Auswertung zeigt sich in diesem Beispiel eine klare Trennung zwischen Normalphase und Ausfall. Hier war die GRU Variante im Training deutlich schneller und erreichte einen niedrigeren Loss. Das Ergebnis hängt vom Datensatz und der Parametrisierung ab, daher ist ein direkter Vergleich unter identischen Bedingungen sinnvoll.
Die folgenden Zeiten stammen aus zwei GPU-Runs (CUDA, NVIDIA GeForce RTX 3080) und dienen nur der Orientierung.
| Modell | X_raw build | Training | Scoring | Finaler Loss |
|---|---|---|---|---|
| TCN | 14.44 s | 114.25 s | 4.40 s | 0.000061 (epoch 25) |
| GRU | 14.42 s | 23.26 s | 4.29 s | 0.000001 (epoch 5, early stop) |
Fazit
Die Deep Learning Variante übernimmt den Residualscore-Gedanken aus Teil 1, ersetzt aber die handgebauten Features durch einen CNN-Encoder. Dadurch lassen sich komplexe Muster in Rohsignalen erfassen, der Preis ist höherer Rechenaufwand, der sich mit GPU gut beherrschen lässt.
Für einfache Fälle reicht der Feature-Ansatz aus. Deep Learning lohnt sich vor allem bei komplexen Signalstrukturen oder mehreren Kanälen. Entscheidend bleiben eine saubere Referenzphase, eine nachvollziehbare Scoredefinition und eine klare Kalibrierung der Schwellen.
Referenzen und Links
- IMS Bearings Dataset (NASA)
- TCN: Bai, Kolter, Koltun (2018), An Empirical Evaluation of Generic Convolutional and Recurrent Networks for Sequence Modeling (arXiv)
- TCN Referenzcode: locuslab/TCN (GitHub)
- GRU: Cho et al. (2014), Learning Phrase Representations using RNN Encoder Decoder for Statistical Machine Translation (arXiv)
- GRU Implementierung: torch.nn.GRU (PyTorch Dokumentation)
Hinweis: Der Beitrag entstand mit Unterstützung von ChatGPT. Inhaltliche Prüfung, Auswahl und Redaktion liegen beim Autor.