Hemisphärische Kugelflächenfunktionen

Mittels der Transformation $\theta \rightarrow 2\,\cos(\theta)-1$, die das Intervall $[0,\pi/2]$ nach $[-1,1]$ abbildet, lassen sich Kugelflächenfunktionen auf der Halbkugel erklären.

Basisfunktionen

Gautron [1] stellt eine Basis aus Kugelflächenfunktionen für die Hemisphäre vor:
$$
\newcommand{\R}{\mathbb{C}}
\newcommand{\R}{\mathbb{R}}
\newcommand{\N}{\mathbb{N}}
\newcommand{\Z}{\mathbb{Z}}
$$
Seien $l \in \N$, $m \in \Z$ mit $|m| \leq l$, $\phi \in [0,2\pi)$ der Azimutwinkel und $\theta \in [0, \pi/2]$ der Polarwinkel.
\begin{equation}
H_l^m: \, [0, \pi/2]\times [0,2\pi) \rightarrow \R , \quad H_l^m(\theta, \phi) := \begin{cases}
\sqrt{2} \, K_l^m \, \cos( m\, \phi) \, \widetilde{P}_l^m( \cos \theta ) & \quad \text{für } m > 0 \\
\sqrt{2} \, K_l^m \, \sin( |m| \, \phi) \, \widetilde{P}_l^{|m|}( \cos \theta ) & \quad \text{für } m < 0 \\ K_l^0 \, \widetilde{P}_l^0( \cos \theta ) & \quad m = 0 \\ \end{cases}
\end{equation}
wobei
$$
\widetilde{P}_l^m( x ) = P_l^m(2\, x-1), \quad x\in [0,1]
$$
die geshifteten assoziierte Legendre-Funktionen, (siehe auch hier) und
$$
K_l^m= \sqrt{ \frac{(2\,l+1)}{ 2 \, \pi } \frac{(l-|m|)!}{(l+|m|)!} }
$$ Normierungsfaktoren sind. Insbesondere ist
$$
K_l^0= \sqrt{ \frac{2\,l+1}{ 2 \, \pi } }, \qquad K_l^m = K_l^{-m}.
$$ Die Funktionen $H_l^m$ werden als hemispherical harmonics, kurz HSH, bezeichnet.

• Die Ansatzfunktionen werden über das Paar $(l,m)$ indiziert; $l$: Grad/degree oder band, $m$ order. $$ \mathcal{I}_{\omega}(n) := \{ (l,m) \, : \, l \in \N , m\in \Z, \text{ mit } l \leq n, \; |m|\leq n \} .$$ Ein Ansatz (wie hier) über die ersten $n+1$ Bänder enthält insgesamt $(n+1)^2$ Basis­funktionen $H_l^m$, d.h. $|\mathcal{I}_{\omega}(n)| = (n+1)^2.$
• Die HSHs sind othonormal: $$ \newcommand{\Spro}[2]{\langle {#1},{#2} \rangle} \Spro{H_l^m}{H_k^n}_{\mathcal{H}^2}:= \int_{\mathcal{H}^2} H_l^m(\theta, \phi) \, H_k^n(\theta, \phi) d\omega = \delta_{lk}\delta_{mn} .$$ Dabei bezeichnet $\mathcal{H}^2 := [0, \pi/2]\times [0,2\pi] $ die Halbkugel.

Plots

Nachfolgend Plots zu den ersten 5 Bändern.

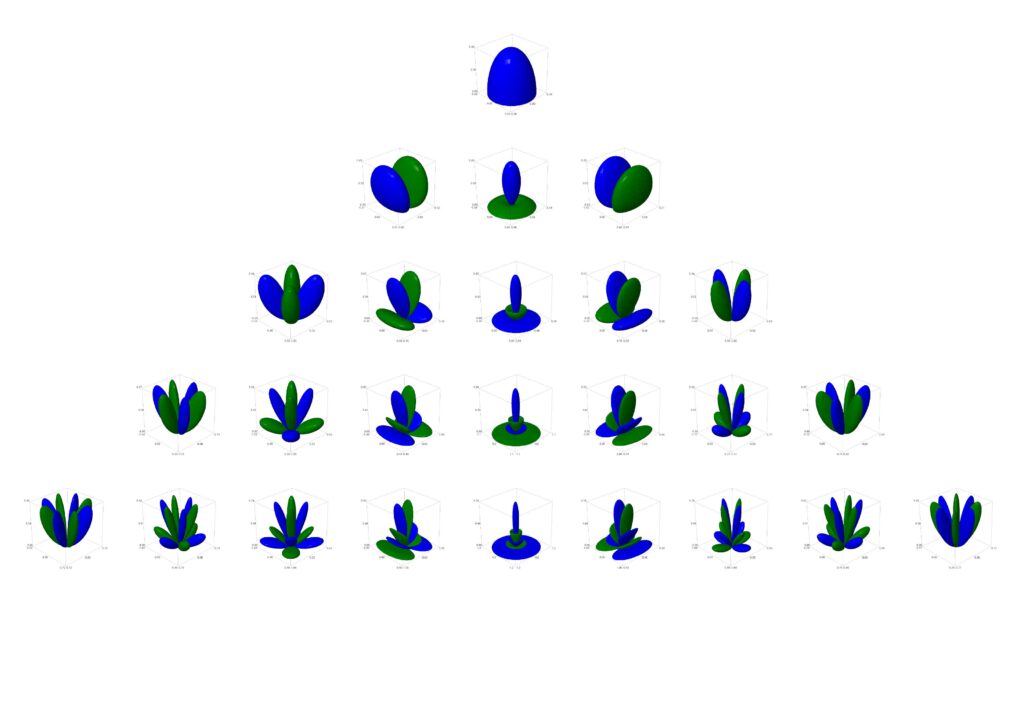
Hier ein entsprechendes SageMath-Script zum Plot der Basisfunktionen.