Anomalieerkennung in Zeitreihen bedeutet: Fortlaufende Mess- und Prozessdaten werden automatisch darauf geprüft, ob das Systemverhalten auffällig vom erwarteten Normalbetrieb abweicht. In technischen Anwendungen betrifft das typischerweise Sensorwerte wie Temperatur, Druck oder Strom, Kennzahlen aus IT- und OT-Monitoring oder Qualitätsmessungen. Der Nutzen liegt darin, Abweichungen frühzeitig zu identifizieren, bevor daraus Ausfälle, Qualitätsprobleme oder kostspielige Folgeschäden entstehen.
In der Praxis sind Anomalien selten nur einzelne Ausreißer. Häufig handelt es sich um Muster über Zeit: ein Drift, eine veränderte Dynamik, ein unerwarteter Betriebszustand oder eine Kombination mehrerer Effekte. Eine reine Grenzwertüberwachung stößt hier schnell an Grenzen, weil Normalbetrieb je nach Last, Umgebung und Betriebsmodus schwankt. Verlässliche Labels („ab hier definitiv defekt“) sind oft nicht verfügbar oder nur unscharf definierbar. Deshalb arbeiten viele Verfahren nicht als einfache Klassifikatoren, sondern bewerten Abweichungen kontinuierlich.
Technisch lässt sich das Thema auf zwei bewährte Grundprinzipien reduzieren:
- Statistik und regelbasierte Verfahren überwachen Kennzahlen in gleitenden Fenstern und reagieren auf signifikante Abweichungen.
- Modellbasierte Verfahren lernen den Normalzustand aus Daten und erzeugen daraus einen Anomalie-Score, etwa über Rekonstruktionsfehler eines Autoencoders oder Vorhersagefehler. Statt „Alarm/kein Alarm“ entsteht ein skalierbarer Score, der Priorisierung und Kalibrierung ermöglicht.
In diesem Beispiel kommen zwei Ansätze zum Einsatz: eine klassische, regelbasierte Baseline (robuste Z-Scores auf RMS/Kurtosis/Bandpower) und eine modellbasierte ML-Variante (Forecast-Residual-Score). Letztere basiert hier auf einer einfachen Ridge-Regression (kein neuronales Netz), die aus Normaldaten ein Vorhersagemodell lernt.
Wesentlich ist die methodisch saubere Bewertung: Training, Kalibrierung und Test werden strikt getrennt, damit Normalisierung und Schwellwerte nicht unbeabsichtigt Informationen aus dem Test sehen. Labels, falls vorhanden, werden nicht zur Optimierung verwendet, sondern ausschließlich zur Evaluation. Zusätzlich werden einfache Baselines mitgeführt, um den Nutzen belastbar einzuordnen.
Fortsetzung: Anomalieerkennung in Zeitreihen, Teil 2: Deep Learning
Beispiel: Vibration / Lager-Testlauf
Das folgende Beispiel demonstriert die Anomalieerkennung auf Vibrationsdaten eines Lager-Testlaufs in kompakter Form. Ausgangspunkt sind hochfrequente Rohsignale als Snapshots. Pro Snapshot werden robuste Features extrahiert, z. B. RMS, Kurtosis und Bandpower. Dabei werden ein statistischer Referenz-Score und ein modellbasierter Forecast-Residual-Score verglichen, optional ergänzt durch einen ML-Gegencheck wie IsolationForest. Die Auswertung wurde in einem Jupyter-Notebook umgesetzt.
Datenquelle: NASA/IMS Bearing Dataset
Die folgenden Ergebnisse basieren auf dem öffentlich verfügbaren IMS Bearing Dataset (Test-to-Failure am Prüfstand). Für das Beispiel wird Set 1 verwendet, weil es einen vollständigen Lauf mit klar dokumentiertem Versuchsaufbau und einer eindeutigen Kanalzuordnung enthält.
- Prüfstand: Vier Wälzlager auf einer Welle, konstante Drehzahl 2000 RPM, radiale Last 26.7 kN, Zwangsschmierung.
- Sensorik: Beschleunigungsaufnehmer am Lagergehäuse; in Set 1 jeweils zwei Achsen pro Lager (insgesamt 8 Kanäle).
- Datenformat: Pro Datei ein 1-Sekunden-Snapshot als ASCII, mit 20480 Messpunkten bei 20 kHz.
- Aufnahmeintervall (Set 1): typischerweise alle 10 Minuten (die ersten 43 Dateien alle 5 Minuten).
-
Umfang (Set 1): 2156 Dateien, Zeitraum 22.10.2003 bis 25.11.2003. Kanalzuordnung:
Bearing 1 = Ch1/Ch2, Bearing 2 = Ch3/Ch4, Bearing 3 = Ch5/Ch6, Bearing 4 = Ch7/Ch8. - Endzustand (Set 1): Inner-Race-Defekt in Lager 3 und Roller-Element-Defekt in Lager 4.
- Messlücken: Größere Zeitabstände in den Dateinamen deuten auf eine Fortsetzung am nächsten Arbeitstag hin.
- Download: IMS.zip (NASA)
Für die weitere Verarbeitung wird jede Datei als Snapshot behandelt und das Rohsignal in robuste Features verdichtet, z. B. RMS, Kurtosis und Bandpower. So entsteht eine Feature-Zeitreihe, die sich für Prognosemodelle und score-basierte Überwachung eignet, ohne Messlücken zu glätten.
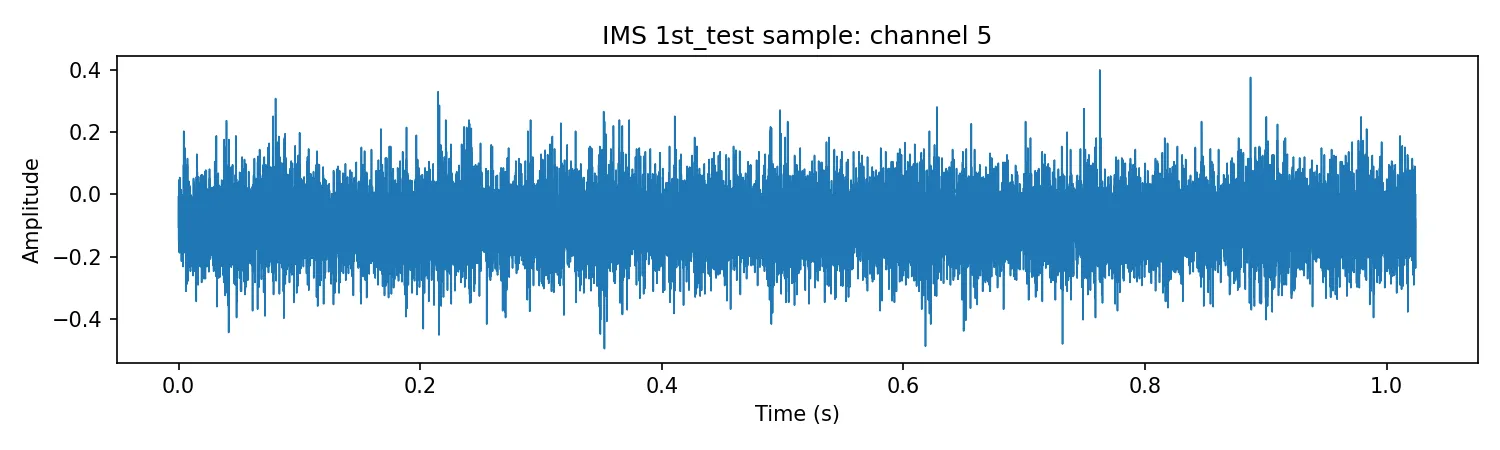
Wie dieses Beispiel zu verstehen ist
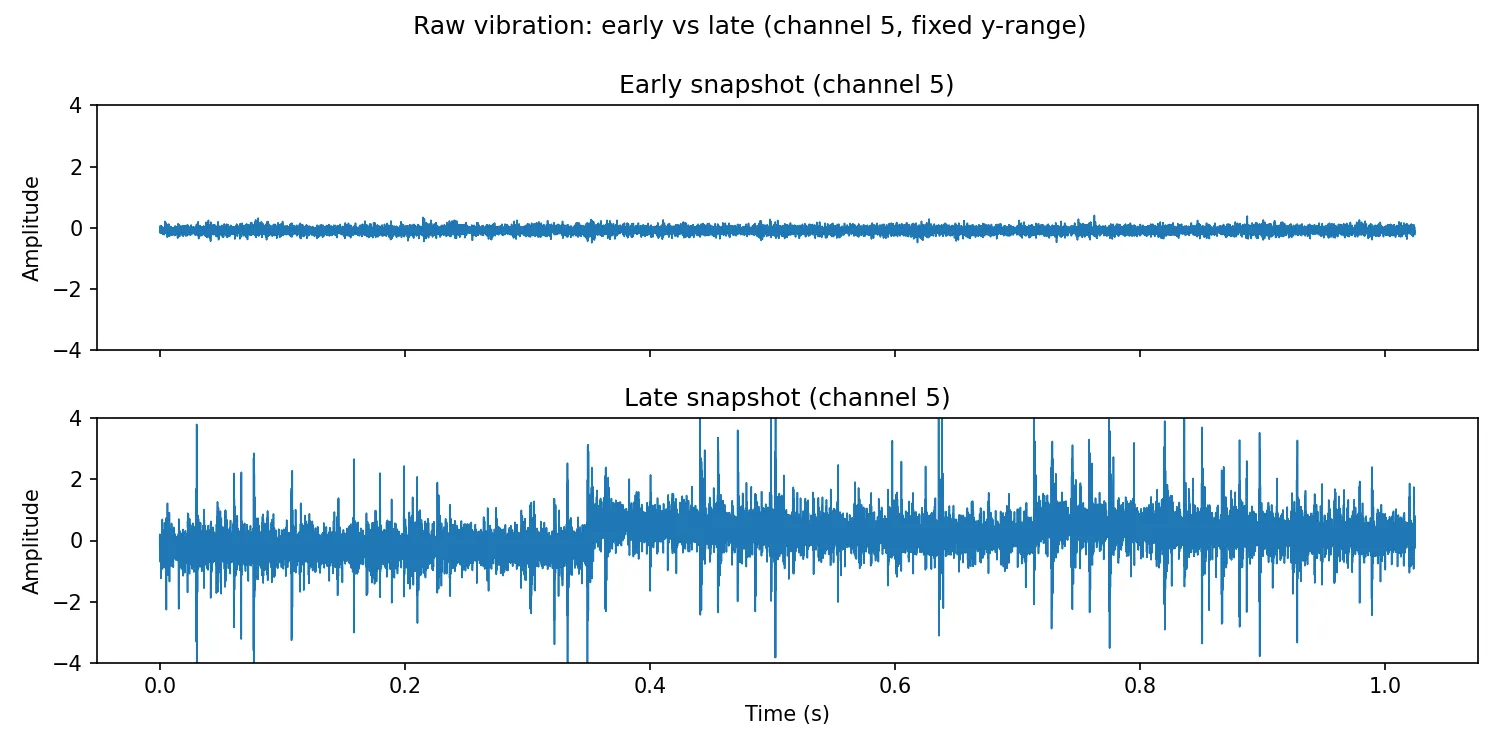
Der IMS-Datensatz ist ein Test-to-Failure-Versuch: Man kennt den Versuchsaufbau und den Endzustand, aber es gibt typischerweise keine eindeutigen Labels pro Snapshot im Sinne von „ab hier definitiv defekt“. Deshalb kommt ein score-basiertes, semi-supervised Vorgehen zum Einsatz.
Die Referenzphase umfasst die ersten 30 % der Snapshots (Modelltraining und Schwellenkalibrierung). Den restlichen Verlauf nutzt die Auswertung ausschließlich zur Bewertung. Details zu Residual-Score und Schwellenwerten folgen in den nächsten Abschnitten.
Setup und Konfiguration
Im Beispiel sind nur wenige Parameter wirklich entscheidend. Sie steuern, welche Phase als Referenz gilt, wie „kurzfristig“ das Prognosemodell arbeitet und auf welchen Kanal bzw. welches Lager wir uns fokussieren.
-
Referenzphase:
train_frac = 0.3– die ersten 30 % werden zur Modell- und Schwellenableitung genutzt. - Ein-Schritt-Forecast: Das Modell prognostiziert jeweils den nächsten Feature-Wert.
-
Lag-Länge:
lag_p = 20– das Modell nutzt die letzten 20 Werte als Kontext (anpassbar). -
Signalwahl: Für das Beispiel reicht ein einzelner Kanal, z. B.
ch5oderch6von Bearing 3.
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from sklearn.linear_model import Ridge
from sklearn.pipeline import Pipeline
from sklearn.preprocessing import StandardScaler
# --- Konfiguration ---
train_frac = 0.3 # Referenzphase: erste 30%
lag_p = 20 # Kontextlänge fürs Forecasting
channel = "ch5" # Beispielkanal (Bearing 3: ch5/ch6)
# Optional (für spätere Schritte):
# q = 0.995 # Quantil für Schwellenwertsetzung ohne Labels
Feature-Extraktion pro Snapshot
Die Rohvibration ist hochfrequent (20 kHz) und liefert pro Snapshot \(N=20480\) Abtastwerte. Für eine robuste Überwachung verdichten wir jeden Snapshot auf wenige, interpretierbare Kennwerte (Features). Dadurch reduziert sich das Datenvolumen erheblich, Messlücken sind unkritisch (Snapshots werden unabhängig verarbeitet), und die späteren Scores lassen sich besser kalibrieren und erklären.
Mathematische Definitionen der Features
Mathematisch sei ein Snapshot durch Abtastwerte \(x_0,\dots,x_{N-1}\) gegeben. Zunächst wird der Mittelwert abgezogen: \[ \bar{x}=\frac{1}{N}\sum_{n=0}^{N-1}x_n,\qquad \tilde{x}_n=x_n-\bar{x}. \] Alle folgenden Features beziehen sich auf \(\tilde{x}_n\).
-
RMS (Root Mean Square):
\[
\mathrm{RMS}=\sqrt{\frac{1}{N}\sum_{n=0}^{N-1}\tilde{x}_n^2}.
\] -
Peak-to-Peak:
\[
\mathrm{P2P}=\max_{0\le n<N}\tilde{x}_n-\min_{0\le n<N}\tilde{x}_n.
\] -
Crest-Factor:
\[
\mathrm{Crest}=\frac{\max_{0\le n<N}\left|\tilde{x}_n\right|}{\mathrm{RMS}}.
\] -
Kurtosis (raw/Pearson, nicht „excess“):
Zunächst die Standardabweichung (population-style)
\[
s=\sqrt{\frac{1}{N}\sum_{n=0}^{N-1}(x_n-\bar{x})^2}
=\sqrt{\frac{1}{N}\sum_{n=0}^{N-1}\tilde{x}_n^2}.
\]
Dann
\[
\mathrm{Kurtosis}=\frac{1}{N}\sum_{n=0}^{N-1}\left(\frac{x_n-\bar{x}}{s}\right)^4
=\frac{1}{N}\sum_{n=0}^{N-1}\left(\frac{\tilde{x}_n}{s}\right)^4.
\]
Hinweis: Eine „excess kurtosis“ wäre \(\mathrm{Kurtosis}-3\). -
Spektral-Schwerpunkt (Spectral Centroid) und Bandpower:
Für Abtastrate \(f_s\) definieren wir die Frequenzbins
\[
f_k=\frac{k}{N}f_s,\qquad k=0,\dots,\left\lfloor\frac{N}{2}\right\rfloor.
\]
Aus der einseitigen Fouriertransformierten \(X_k\) (hier via rFFT, typischerweise mit Fensterung)
verwenden wir ein Leistungsspektrum
\[
P_k=\frac{|X_k|^2}{N}
\]
(Konstanten sind für Zeitvergleiche unerheblich). Dann
\[
f_c=\frac{\sum_k f_k\,P_k}{\sum_k P_k}
\]
und für ein Frequenzband \([f_a,f_b)\)
\[
\mathrm{BP}[f_a,f_b)=\sum_{k:\,f_a\le f_k<f_b}P_k.
\]
Im Beispiel: \([0,1\text{ kHz}),[1,3\text{ kHz}),[3,10\text{ kHz})\).
Der folgende Codeblock zeigt die Kernfunktionen zur Feature-Berechnung. In der Auswertung wird diese Funktion auf jeden Snapshot angewandt und das Ergebnis als Zeile in einer Feature-Tabelle gespeichert.
import numpy as np
def kurtosis_np(x: np.ndarray) -> float:
"""Raw/Pearson Kurtosis (nicht excess)."""
x = np.asarray(x)
m = x.mean()
v = np.mean((x - m) ** 2) # entspricht s^2 mit 1/N
if v == 0:
return 0.0
m4 = np.mean((x - m) ** 4)
return float(m4 / (v ** 2))
def spectral_features(x: np.ndarray, fs: float = 20000.0):
"""Spektral-Schwerpunkt + Bandenergien (einseitig)."""
x = np.asarray(x)
n = len(x)
w = np.hanning(n)
X = np.fft.rfft(x * w)
P = (np.abs(X) ** 2) / n
f = np.fft.rfftfreq(n, d=1.0 / fs)
def bandpower(lo, hi):
mask = (f >= lo) & (f < hi)
return float(P[mask].sum())
centroid = float((f * P).sum() / (P.sum() + 1e-12))
return centroid, bandpower(0, 1000), bandpower(1000, 3000), bandpower(3000, 10000)
def extract_features_from_snapshot(x: np.ndarray, fs: float = 20000.0) -> dict:
"""Feature-Vektor für einen Snapshot (1 Sekunde)."""
x = np.asarray(x)
x = x - x.mean()
rms = float(np.sqrt(np.mean(x ** 2)))
peak = float(np.max(np.abs(x)))
crest = float(peak / (rms + 1e-12))
p2p = float(x.max() - x.min())
kur = float(kurtosis_np(x))
centroid, bp0, bp1, bp2 = spectral_features(x, fs=fs)
return {
"rms": rms,
"crest": crest,
"kurtosis": kur,
"p2p": p2p,
"spec_centroid": centroid,
"bp_0_1k": bp0,
"bp_1_3k": bp1,
"bp_3_10k": bp2,
}
Ergebnis ist eine Feature-Tabelle df_feat mit einer Zeile pro Snapshot. Bei mehreren Kanälen werden die Spalten entsprechend benannt (z. B. rms_ch5, kurtosis_ch5, …). Im nächsten Schritt wählen wir eine Feature-Reihe (z. B. rms_ch5) und erzeugen daraus die Residual-Scores.
Forecasting und Residual-Score
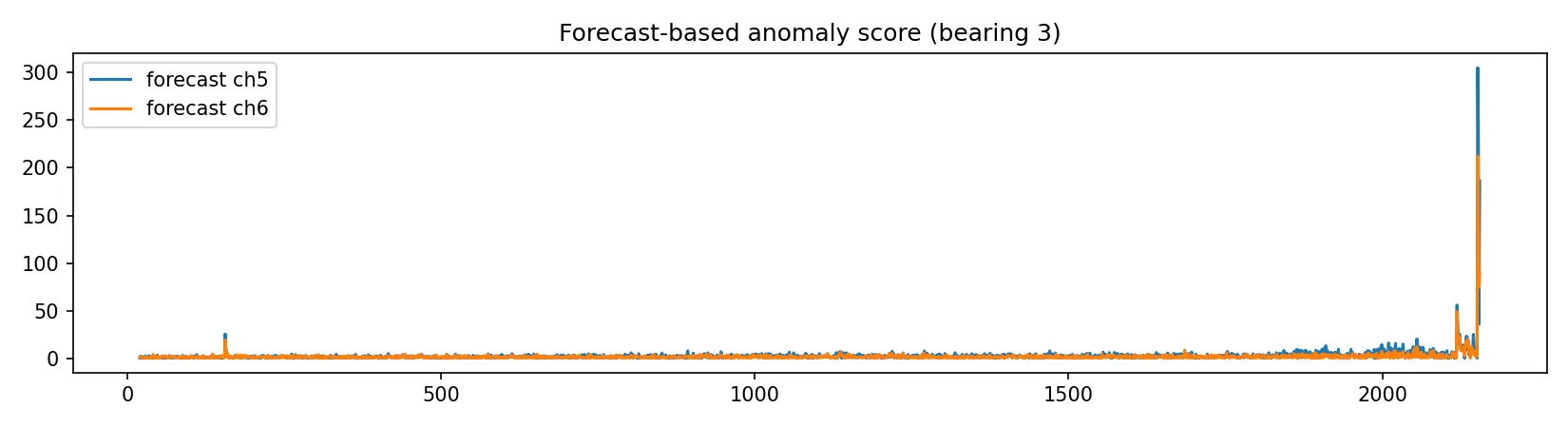
Kernidee des Ansatzes: Wir lernen aus der Referenzphase ein Modell für das erwartete Normalverhalten einer Feature-Zeitreihe, z. B. \(y_t=\mathrm{RMS}(t)\). Anschließend prognostizieren wir fortlaufend den nächsten Wert und bewerten den Vorhersagefehler (Residual). Wenn sich das Systemverhalten ändert (z. B. beginnende Schädigung), steigen die Residuen – das liefert einen gut erklärbaren, kontinuierlichen Anomalie-Score.
Formal: Lag-Darstellung und Ridge-Modell
Formal verwenden wir eine Lag-Darstellung: Für eine Lag-Länge \(p\) definieren wir den Eingangsvektor \[ \mathbf{x}_t = \bigl(y_{t-p},\,y_{t-p+1},\,\dots,\,y_{t-1}\bigr)^\top \in \mathbb{R}^p, \] und modellieren \[ \hat{y}_t = f(\mathbf{x}_t). \] Als transparentes Normalmodell dient eine regularisierte lineare Regression (Ridge), \[ \hat{y}_t = \beta_0 + \boldsymbol{\beta}^\top \mathbf{x}_t, \] wobei \((\beta_0,\boldsymbol{\beta})\) ausschließlich auf der Referenzphase \(\mathcal{T}_{\mathrm{ref}}\) bestimmt werden: \[ (\beta_0,\boldsymbol{\beta})=\arg\min_{\beta_0,\boldsymbol{\beta}} \sum_{t\in\mathcal{T}_{\mathrm{ref}}}\bigl(y_t-(\beta_0+\boldsymbol{\beta}^\top\mathbf{x}_t)\bigr)^2 +\lambda\|\boldsymbol{\beta}\|_2^2 . \] Eine Standardisierung der Eingänge wird eingesetzt, um die Regression numerisch stabil zu halten.
Das Residual ist \[ r_t = y_t – \hat{y}_t. \] Daraus definieren wir einen robusten Residual-Score über Median und MAD in der Referenzphase: \[ m = \mathrm{median}(r_t\mid t\in\mathcal{T}_{\mathrm{ref}}),\qquad \mathrm{MAD} = \mathrm{median}\bigl(|r_t-m|\mid t\in\mathcal{T}_{\mathrm{ref}}\bigr), \] \[ s_t = \frac{|r_t-m|}{\mathrm{MAD}+\varepsilon}, \] mit kleinem \(\varepsilon>0\) zur Stabilisierung. Hohe Werte von \(s_t\) bedeuten: Der aktuelle Messwert ist für das gelernte Normalmodell „unerwartet“.
Der folgende Codeblock zeigt die wesentlichen Schritte: Lag-Matrix aufbauen, Ridge-Modell in der Referenzphase fitten, Residuen berechnen und robust normieren.
import numpy as np
from sklearn.linear_model import Ridge
from sklearn.pipeline import Pipeline
from sklearn.preprocessing import StandardScaler
def make_lag_matrix(y: np.ndarray, p: int):
X, Y = [], []
for t in range(p, len(y)):
X.append(y[t-p:t])
Y.append(y[t])
return np.asarray(X), np.asarray(Y)
# Beispiel: RMS als Zielreihe
y = df_feat["rms_ch5"].to_numpy() # ggf. rms_ch6 oder anderes Feature wählen
X, Y = make_lag_matrix(y, p=lag_p)
n_train = int(train_frac * len(Y)) # Referenzphase bezogen auf Y (ab lag_p)
model = Pipeline([
("scaler", StandardScaler()),
("ridge", Ridge(alpha=1.0))
])
model.fit(X[:n_train], Y[:n_train])
Yhat = model.predict(X)
res = Y - Yhat
med = np.median(res[:n_train])
mad = np.median(np.abs(res[:n_train] - med)) + 1e-12
score_res = np.abs(res - med) / mad # hoch = auffällig
Hinweis: Wegen der Lag-Darstellung beginnt die Residual-Zeitreihe erst ab Index \(t=p\). Für die Visualisierung wird der Score daher gegen die Snapshot-Indizes ab \(p\) aufgetragen.
Schwellenwertsetzung ohne Labels
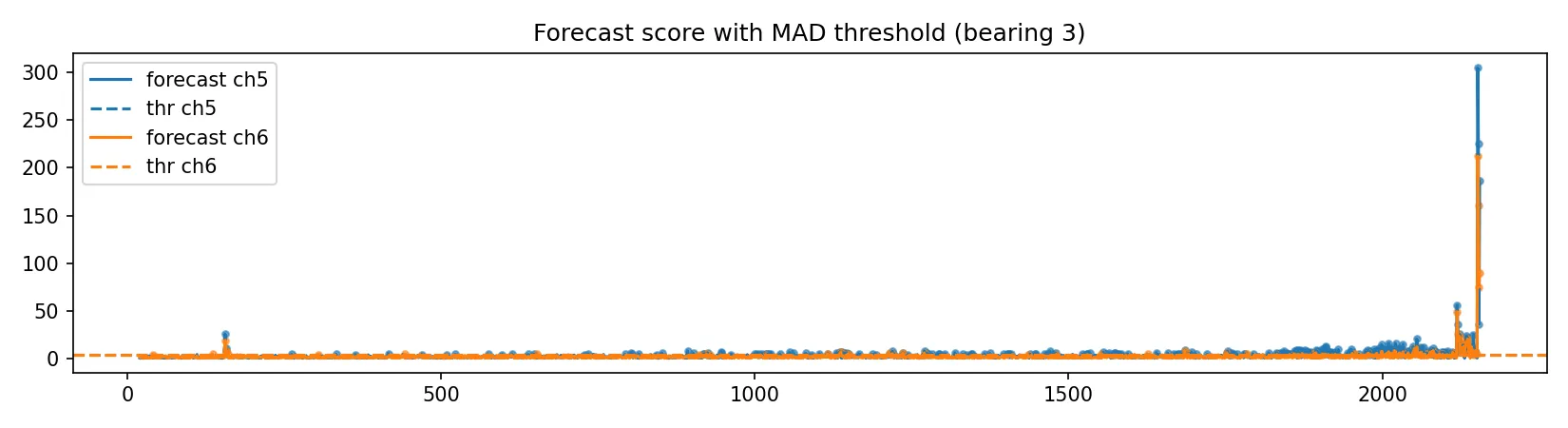
In vielen technischen Anwendungen fehlen belastbare Labels („ab hier definitiv defekt“). Stattdessen wird die Alarmierung aus der Referenzphase abgeleitet: Wir wählen einen Schwellwert so, dass im Normalbetrieb nur selten Fehlalarme auftreten. Das entspricht einer kontrollierten Alarmrate.
Für den Residual-Score \(s_t\) ist ein pragmatischer Ansatz die Schwelle über ein hohes Quantil der Referenzverteilung (z. B. 99,5 %): \[ \tau = Q_q\bigl(s_t\mid t\in\mathcal{T}_{\mathrm{ref}}\bigr), \] wobei \(Q_q\) das \(q\)-Quantil bezeichnet (z. B. \(q=0{,}995\)). Ein Zeitpunkt gilt als auffällig, wenn \(s_t > \tau\). Alternativ wird häufig eine MAD-basierte Schwelle in der Form \[ \tau = \mathrm{median}(s_t\mid \mathcal{T}_{\mathrm{ref}}) + k\cdot \mathrm{MAD}(s_t\mid \mathcal{T}_{\mathrm{ref}}) \] verwendet; beide Varianten sind transparent und ohne Labels umsetzbar.
Für die Praxis ist zusätzlich eine zeitliche Glättung sinnvoll, damit einzelne Peaks nicht sofort als Alarm interpretiert werden. Typischerweise gilt: (a) Alarm erst nach \(m\) Überschreitungen innerhalb eines Fensters, (b) Mindestdauer oberhalb der Schwelle, (c) Zusammenfassung benachbarter Auffälligkeiten zu Intervallen. Im ersten Schritt genügt die einfache Punkt-Entscheidung, weil sie am leichtesten nachvollziehbar ist.
Der folgende Codeblock zeigt die Schwellenwertsetzung über ein Quantil in der Referenzphase und die Markierung auffälliger Zeitpunkte. (Die konkrete Wahl von q ist eine Betriebsentscheidung: je höher q, desto weniger Fehlalarme, aber desto später reagiert das System.)
import numpy as np
# score_res: Residual-Score aus dem Forecasting
# n_train: Länge der Referenzphase (bezogen auf score_res)
q = 0.995
thr = np.quantile(score_res[:n_train], q)
is_anom = score_res > thr
anom_idx = np.where(is_anom)[0] # Indizes beziehen sich auf score_res (ab lag_p)
Fazit und Einordnung
Mit der Kombination aus Feature-Extraktion (pro Snapshot) und Forecast-Residual-Score erhält man ein einfach erklärbares Frühwarnsignal: Das Modell lernt den Normalbetrieb aus einer Referenzphase und meldet Abweichungen dort, wo der aktuelle Verlauf für das Normalmodell unerwartet wird. Das ist besonders nützlich, wenn – wie häufig in der Praxis – keine verlässlichen Labels vorliegen.
Im IMS-Datensatz zeigt sich das typische Run-to-Failure-Muster: Feature-Verläufe wie RMS, Kurtosis und Bandpower verändern sich zum Ende hin, und der Residual-Score steigt deutlich an. Eine Schwelle aus der Referenzphase markiert diese Phase als auffällig, ohne dass explizite Fehlerlabels nötig sind.
Für den produktiven Einsatz hängt der Übergang vom Score zur Alarmierung vom Anwendungsfall ab. Schwellen (Quantil/MAD), Alarmfenster und Re-Training-Zyklen sollten so gewählt werden, dass Fehlalarme und Übersehen zum jeweiligen Risiko- und Kostenprofil passen. Der Ansatz eignet sich als Blaupause für weitere Datenpipelines.
Die vollständige, reproduzierbare Auswertung (inklusive Code, Parameter und aller Plots) ist verfügbar; im Blog werden nur die Schritte gezeigt, die für das Verständnis des Vorgehens notwendig sind.
Weiterlesen: Teil 2 zur Deep Learning Variante: CNN-Encoder, Forecast im Merkmalsraum und Residual-Score.