Key words: Scheduling, combinatorial optimization
Ablaufplanung (Scheduling) ist die Optimierung von Reihenfolgen und Ressourcenzuordnungen unter Kapazitätsrestriktionen. Das Beispiel zeigt, wie stark sich makespan und Auslastung durch gute Planung verbessern lassen.
Das Problem
Gegeben sei eine Menge von Arbeitsaufträgen und bestimmte Ressourcen mit beschränkter Kapazität. Jeder Auftrag besteht aus einer Anzahl von Aktivitäten (auch Operationen oder Task genannt), die evtl. in einer vorgegebenen Reihenfolge abzuarbeiten sind. Dabei bindet jede Operation bei ihrer Ausführung bestimmte Ressourcen. Gesucht ist ein unter betriebswirtschaftlichen Aspekten möglichst optimaler Ablaufplan.
Ausgehend von einem mathematischen Modell kann die Aufgabe als Reihenfolgeproblem formuliert werden. Idealisierte Probleme dieses Typs sind die Job-Shop-Probleme und deren Varianten. Für sie ist bekannt, dass sie NP-schwer sind. Damit ist kein polynomialer Algorithmus zu erwarten, der für alle Instanzen optimale Pläne berechnet. In der Praxis sucht man daher in der Regel nicht nach einer garantiert optimalen Lösung, sondern beschränkt sich darauf, zulässige und möglichst gute Lösungen zu finden und diese schrittweise zu verbessern.
Methodisch liegt die Ablaufplanung damit in der gleichen Familie wie klassische kombinatorische Probleme, bei denen heuristische lokale Suche dominiert. Ein anschauliches Referenzbeispiel ist das Traveling Salesman Problem (TSP).
In logistischen Anwendungen entsprechen Arbeitsaufträge typischerweise Belieferungen oder Versandaufträgen, Aktivitäten einzelnen Prozessschritten wie Kommissionierung, Umschlag oder Verladung und Ressourcen den verfügbaren Kapazitäten in Lager, Personal oder Transport. Das dargestellte Modell ist damit strukturell identisch zu operativen Planungsproblemen in Logistiknetzwerken.
Ein einfaches Beispiel zur Ablaufplanung (Scheduling)
Das folgende Szenario ist ein bewusst vereinfachtes Beispiel und dient der Veranschaulichung der Ablaufplanung.
Ein Logistikteam aus 4 Mitarbeitenden soll drei Versandaufträge (Jobs)
\[J_1 = \{O_1, O_2, O_3, O_4\}, \; J_2 = \{O_5, O_6, O_7\} \; \text{und} \; J_3 = \{O_8, O_9\}\]
so schnell wie möglich abwickeln. Jede einzelne Operation erfordert bestimmte Ressourcen (Mitarbeitende) und eine bestimmte Durchführungsdauer. Gefordert ist dann die Minimierung der Gesamtbearbeitungszeit für die Versandaufträge, der sogenannte makespan.
| Job | j | Aktion | Dauer [min] | MA |
|---|---|---|---|---|
| \(J_1\) | 1 | \(O_1\) | 20 | 1 |
| 2 | \(O_2\) | 40 | 2 | |
| 3 | \(O_3\) | 10 | 1 | |
| 4 | \(O_4\) | 80 | 3 | |
| \(J_2\) | 5 | \(O_5\) | 30 | 2 |
| 6 | \(O_6\) | 20 | 1 | |
| 7 | \(O_7\) | 15 | 3 | |
| \(J_3\) | 8 | \(O_8\) | 60 | 1 |
| 9 | \(O_9\) | 90 | 1 |
Die Aktivitäten sind nicht unabhängig voneinander ausführbar, sondern es muss eine bestimmte Reihenfolge eingehalten werden, die mittels der sogenannten Vorrangrelation gegeben ist. Der nachfolgende Graph (ein gerichteter azyklischer Graph, DAG) definiert die Vorrangrelation für dieses Beispiel. So kann z.B. Operation \(O_3\) erst starten, wenn \(O_2\) (Freigabe) und \(O_5\) (Materialbereitstellung) abgeschlossen sind, während \(O_1\) und \(O_6\) unabhängig voneinander sind.
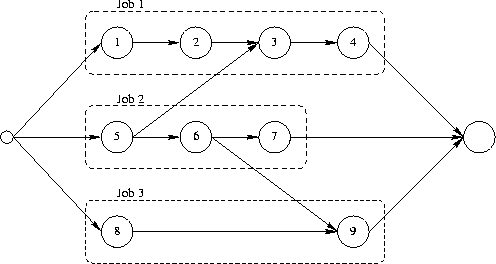
Das Optimierungsziel wird durch die Endzeiten der Operationen \(O_4\), \(O_7\) und \(O_9\) festgelegt: Ist \(s_i\) die Startzeit der i-ten Operation (\(O_1\) startet zum Zeitpunkt \(s_1\) usw.), dann gilt: \[ \text{makespan} = \max\{s_4 + 80,\; s_7 + 15,\; s_9 + 90\}. \]
Auswertung
- Insgesamt gibt es erstaunliche 362880 möglichen Anordnungen der Operationen. Davon sind aber nur 810 zulässige Pläne, d.h. sie erfüllen die Vorrangrelation. Von den 810 zulässigen Plänen wiederum sind nur 10% optimal.
- Unter der Voraussetzung, dass eine Aktivität O begonnen wird, falls
- alle Vorgänger beendet und
- genügend Gruppenmitglieder (Ressourcen) zur Durchführung von O frei sind
ergeben sich die Zeiten und Vergleiche der nachfolgenden Tabelle:
| Plan | makespan [min] | Differenz zu \(S_0\) [min] |
|---|---|---|
| bester Plan \(S_0\) | 170 | – |
| schlechter Plan \(S_B\) | 220 | 50 (23%) |
| Erwartungswert | 184 | 14 (7.6%) |
Gegenüber einem schlechten Plan, dieser sei mit \(S_B\) bezeichnet, bei dem das Team mit 4 Mitgliedern 50 Minuten mehr benötigt, als wenn es nach \(S_0\) vorgeht, ist durch die Optimierung die Leistungsfähigkeit der Gruppe um ca. 23% erhöht worden. Wird aus allen zulässigen Plänen zufällig einer ausgewählt, so ist der Erwartungswert des makespans 184 min. Ein optimaler Plan ist durchschnittlich noch 7.6% besser.
Ressourcenauslastung im Vergleich
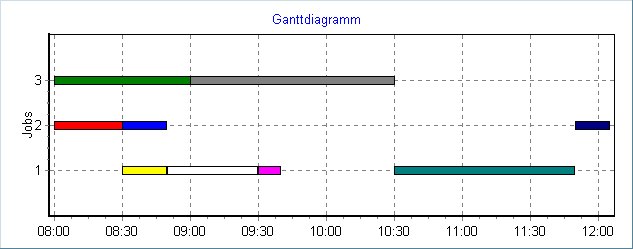
Die beiden nächsten Grafiken zeigen die Ressourcenauslastung bzgl. \(S_0\) und \(S_B\). Man sieht sofort, dass ein Vorgehen nach dem zweiten Plan alles andere als gut ist, was auch an der Einfachheit des Beispiels liegt: die vorgegebene Situation ist noch recht übersichtlich.
Im Fall \(S_0\) werden die Versandaufträge im Zeitraum von 8:00 bis 10:50 vollständig bearbeitet und alle Mitglieder der Gruppe sind durchgehend gut beschäftigt (insgesamt 55 min “Leerlauf”). Während eine Arbeitsorganisation nach \(S_B\) erst um 11:40 fertig ist und immerhin 255 min “Untätigkeit” für die Arbeitsgruppe erzeugt.
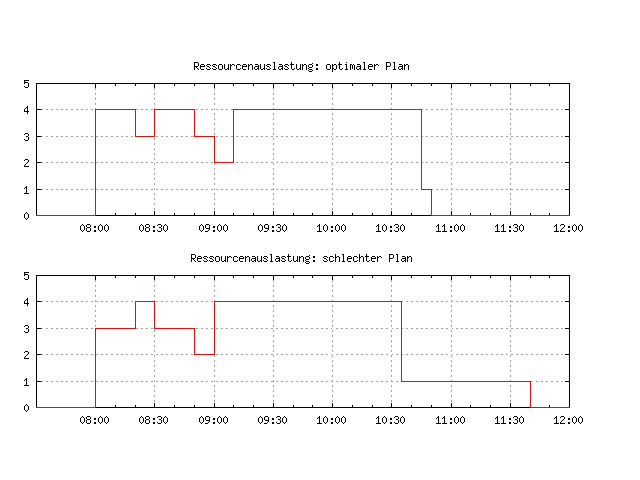
Das Team muss aus mindestens 3 Mitgliedern bestehen, da die Aktivitäten \(O_7\) und \(O_4\) in diesem Beispiel nur von 3 Mitarbeitenden gemeinsam ausgeführt werden können. Wie sehen nun die Ergebnisse für eine Gruppe mit nur 3 Arbeitern aus?
| Plan | makespan [min] | Differenz zu \(S_0\) [min] |
|---|---|---|
| bester Plan \(S_0\) | 245 | – |
| schlechter Plan \(S_B\) | 345 | 100 (29%) |
| Erwartungswert | 284 | 39 (13.7%) |
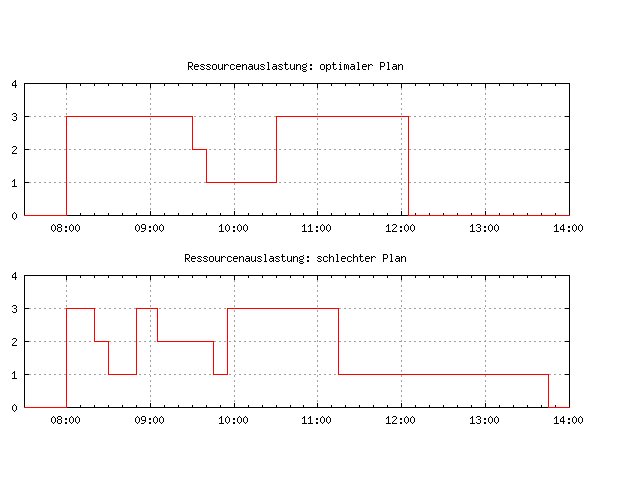
Das Team mit 3 Mitgliedern benötigt mindestens 245 min zur Bewältigung der Arbeitsaufträge, kann diese aber auch bei schlechter Planung 100 min später abgeschlossen haben, d.h. bzgl. des Optimierungsziels makespan, ist \(S_0\) 29% besser als \(S_B\).
Anmerkung
Für dieses einfache Beispiel ist es übrigens “schwieriger” die schlechten Pläne zu finden. Wählt man aus den 810 zulässigen Plänen zufällig einen aus, so liegen der Erwartungswert für die Bearbeitungszeit der 3 Jobs näher an der eines optimalen Plans, als an den Zeiten für die “schlechten” Pläne. Aber natürlich ist der durch die Optimierung gefundene Plan \(S_0\) einem zufällig ausgewählten Plan überlegen: durchschnittlich hat man eine Effizienzsteigerung um 7.6% bzw. 13.7%.
Einordnung aus Sicht des Operations Research
Das Beispiel zeigt, dass bereits einfache Scheduling-Modelle erhebliche Effizienzunterschiede erzeugen können. In der Praxis bilden solche Modelle häufig den Kern datengetriebener Entscheidungsunterstützung – etwa bei der Planung von Logistiknetzwerken, Standortauslastungen oder Szenarioanalysen unter Kapazitätsrestriktionen. Die hier verwendete Modellierungslogik lässt sich direkt auf größere Netzwerke und komplexere Planungsprobleme übertragen.
Quelle des Originaltexts: Web Archive (2005)
AMS Subject Classifications: 90Bxx